练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】张大伯从报社以每份0.4元的价格购进了份报纸，以每份0.5元的价格售出了份报纸，剩余的以每份0.2元的价格退回报社，则张大伯卖报收入（）元

    A. 0.7b-0.6a B. 0.5b-0.2a C. 0.7b-0.6a D. 0.3b-0.2a

    【答案】D

    【解析】

    张大伯购进报纸共花费了0.4a元，售出的报纸共得0.5b元,退回报社的报纸共得0.2(a-b)元,所以张大伯卖报共收入0.5b+0.2(a-b)-0.4a=0.3b-0.2a（元）.

    因为张大伯购进报纸共花费了0.4a元,售出的报纸共得0.5b元,退回报社的报纸共得0.2（a-b）元,

    所以张大伯卖报收入0.5b+0.2（a-b）-0.4a=0.3b-0.2a.

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC内接于⊙O，AB、CD为⊙O直径，DE⊥AB于点E，sinA= ，则∠D的度数是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

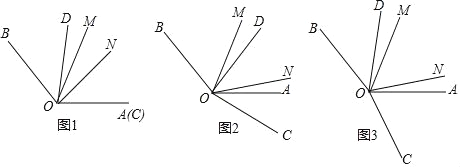
    【题目】已知∠AOB＝130°，∠COD＝80°，OM，ON分别是∠AOB和∠COD的平分线．

    (1)如果OA，OC重合，且OD在∠AOB的内部，如图1，求∠MON的度数；

    (2)如果将图1中的∠COD绕点O点顺时针旋转n°(0＜n＜155)，如图2，

    ①∠MON与旋转度数n°有怎样的数量关系？说明理由；

    ②当n为多少时，∠MON为直角？

    (3)如果∠AOB的位置和大小不变，∠COD的边OD的位置不变，改变∠COD的大小；将图1中的OC绕着O点顺时针旋转m°(0＜m＜100)，如图3，∠MON与旋转度数m°有怎样的数量关系？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

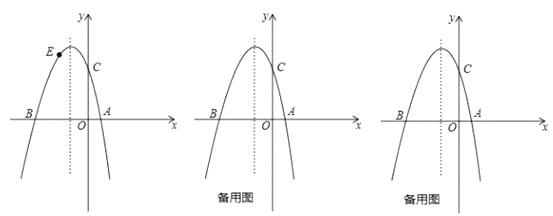
    【题目】如图，已知已知抛物线 与x轴交于点 和点 ，与y轴交于点C，且 .

    （1）求此抛物线的解析式；
    （2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；
    （3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标.
    （4）连AC，H是抛物线上一动点，过点H作AC的平行线交x轴于点F，是否这样的点F，使得以A,C,H,F为顶点的四边形是平行四边形？若存在，直接写出满足条件的点F的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为a的正方形木块在水平地面上沿直线滚动一周（没有滑动），则它的中心点O所经过的路径长为（ ）

    A.4a
    B.2 πa
    C.
    πa
    D.
    a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有四张规格、质地相同的卡片，它们背面完全相同，正面图案分别是A．平行四边形，B．菱形，C．矩形，D．正方形，将这四张卡片背面朝上洗匀后．
    （1）随机抽取一张卡片图案是轴对称图形的概率是；
    （2）随机抽取两张卡片（不放回），求两张卡片卡片图案都是轴对称图形的概率，并用树状图或列表法加以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读）|4﹣1|表示4与1差的绝对值，也可以理解为4与1两数在数轴上所对应的两点之间的距离；|4+1|可以看做|4﹣（﹣1）|，表示4与﹣1的差的绝对值，也可以理解为4与﹣1两数在数轴上所对应的两点间的距离．

    （1）|4﹣（﹣1）|=　 　

    （2）|5+2|=　 　

    （3）利用数轴找出所有符合条件的整数x，使得|x+3|=5，则x=　 　．

    （4）利用数轴找出所有符合条件的整数x，使得|x+3|+|x﹣2|=5，这样的整数是：　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．

    （1）请判断：FG与CE的关系是___；

    （2）如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；

    （3）如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+ x+c（a≠0）与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知点A的坐标为（﹣1，0），点C的坐标为（0，2）．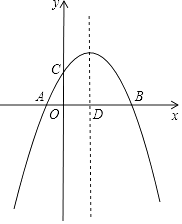

    （1）求抛物线的解析式；
    （2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
    （3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

    查看答案和解析>>

    同步练习册答案