
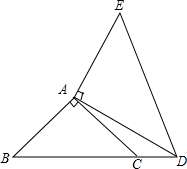
 如图,△ABC是等腰直角三角形,在BC的延长线上取一点D,连接AD,以AD为腰作等腰直角△DAE,若BC=3,CD=1,求AD的长.
如图,△ABC是等腰直角三角形,在BC的延长线上取一点D,连接AD,以AD为腰作等腰直角△DAE,若BC=3,CD=1,求AD的长.科目:初中数学 来源: 题型:
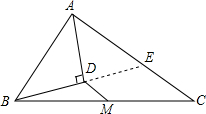 △ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
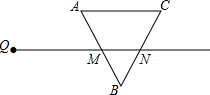 射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,这时CD与AB有什么关系?为什么?
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,这时CD与AB有什么关系?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com