
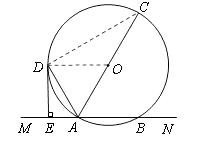
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
【答案】
(1)证明:连接OD,
∵OA=OD,∴∠OAD=∠ODA。
∵∠OAD=∠DAE,∴∠ODA=∠DAE。∴DO∥MN,
∵DE⊥MN,∴∠ODE=∠DEM =90°,即OD⊥DE。
∵D在⊙O上,∴DE是⊙O的切线
(2)解:连接CD,
 ,
,
∵∠AED=90°,DE=6,AE=3,∴AD= ![]() ,
,
∵AC是⊙O的直径,∴∠ADC=∠AED =90°。
∵∠CAD=∠DAE,∴△ACD∽△ADE。 ∴ ![]() ,即
,即 ![]() 。
。
解得:AC=15,
∴⊙O的半径是7.5cm。
【解析】 (1)要证DE是⊙O的切线,因此连接OD,先根据OA=OD得出∠OAD=∠ODA,由AD平分∠CAM得出∠OAD=∠DAE,再证出∠ODA=∠DAE得到DO∥MN,由DE⊥MN,证得OD⊥DE。即可得出结论。
(2)根据已知易证△ACD∽△ADE,根据相似三角形的对应边成比例,建立方程求解即可。
【考点精析】掌握平行线的性质和等腰三角形的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬买了A、B两种书,单价分别是18元、10元.
(1)若两种书共买了10本付款172元,求每种书各买了多少本?
(2)买10本时付款可能是123元吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
户 数 | 1 | 1 | 2 | 4 |
这20个家庭的年平均收入为 万元;
(2)样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为a,点B对应的数为b,且多项式﹣![]() x2y﹣
x2y﹣![]() xy2﹣2xy+5的次数为a,常数项为b.
xy2﹣2xy+5的次数为a,常数项为b.
(1)直接写出a、b的值;
(2)数轴上点A、B之间有一动点P(不与A、B重合),若点P对应的数为x,试化简:|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 若 ![]() , 求
, 求 ![]() 的值.
的值.
(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,
CG和EH的数量关系是 , ![]() 的值是 .
的值是 .
(2)类比延伸:如图2,在原题条件下,若 ![]() (m>0)则
(m>0)则 ![]() 的值是(用含有m的代数式表示),试写出解答过程 .
的值是(用含有m的代数式表示),试写出解答过程 .
(3)拓展迁移:如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若 ![]() (a>0,b>0)则
(a>0,b>0)则 ![]() 的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
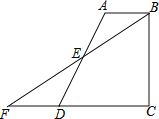
(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数 ![]() 使得在计算
使得在计算 ![]() 的过程中,各数位不产生进位现象,则称
的过程中,各数位不产生进位现象,则称 ![]() 为“本位数.现从所有大于0,且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为= .
为“本位数.现从所有大于0,且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com