
分析 作DE⊥AB于E,先由锐角三角函数求出菱形的高DE,菱形的面积为AB•DE.
解答 解:作DE⊥AB于E,如图所示: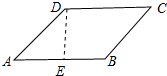 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AD=AB=5,
∵∠DEA=90°,
∴DE=AD•sin45°=5×$\frac{\sqrt{2}}{2}$=$\frac{5\sqrt{2}}{2}$,
∴菱形ABCD的面积=AB•DE=5×$\frac{5\sqrt{2}}{2}$=$\frac{25\sqrt{2}}{2}$;
故答案为:$\frac{25\sqrt{2}}{2}$.
点评 本题考查了菱形的性质、锐角三角函数、菱形面积的计算;根据锐角三角函数求出菱形的高是解决问题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.
小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=$4\sqrt{3}$cm,AD=8cm,直线EF从点A出发沿AD方向匀速运动,速度是2cm/s,运动过程中始终保持EF∥AC,EF交AD于E,交DC于点F;同时,点P从点C出发沿CB方向匀速运动,速度是1cm/s,连接PE、PF,设运动时间为t(s)(0<t<4).
如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=$4\sqrt{3}$cm,AD=8cm,直线EF从点A出发沿AD方向匀速运动,速度是2cm/s,运动过程中始终保持EF∥AC,EF交AD于E,交DC于点F;同时,点P从点C出发沿CB方向匀速运动,速度是1cm/s,连接PE、PF,设运动时间为t(s)(0<t<4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com