
【题目】如图,将菱形ABCD放置在平面直角坐标系中,已知A(0,3).B(﹣4,0)
(1)求经过点C的反比例函数解析式;
(2)设P是(1)中所求函数图象上的一点,以P、O、A为顶点的三角形的面积与△COD的面积相等,求点P的坐标.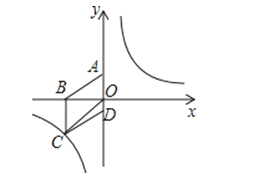
【答案】解:(1)由题意知,OA=3,OB=4
在Rt△AOB中,AB=![]() =5
=5
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(﹣4,﹣5).
设经过点C的反比例函数的解析式为y=![]() (k≠0),
(k≠0),
则k=﹣4×﹣5=20.
故所求的反比例函数的解析式为y=![]() .
.
(2)设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S△COD=![]() ×4×2=4,
×4×2=4,
即![]() AO×|x|=4,
AO×|x|=4,
∴|x|=![]() ,
,
∴x=±![]() ,
,
当x=![]() 时,y=
时,y=![]() ,当x=﹣
,当x=﹣![]() 时,y=﹣
时,y=﹣![]() ,
,
点P的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式;
(2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,以下结论:
的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若点A(﹣1,h),B(2,k)在图象上,则h<k;
④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.
其中正确结论的个数是( )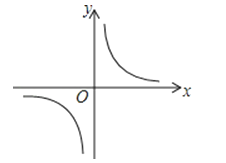
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:

如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后任意摸出两张.

(1)用树状图(或列表法)表示所摸的两张牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌的牌面图形一定能组合成轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子正确的是( )
A.(a﹣b)2=a2﹣2ab+b2
B.(a﹣b)2=a2﹣b2
C.(a﹣b)2=a2+2ab+b2
D.(a﹣b)2=a2﹣ab+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(m,6)在第一象限,且P是反比例函数y=![]() (k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
(k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com