已知:如图.直线y =+1与x轴.y轴的交点分别是A和B.把线段AB绕点A顺时针旋转90°得线段AB＇.⑴ 在图中画出△ABB＇.并直接写出点A和点B＇的坐标, ⑵ 求直线AB＇表示的函数关系式,⑶ 若动点C(1.a)使得S△ABC=S△ABB＇.求a的值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

（10分）已知：如图，直线y =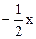+1与x轴、y轴的交点

分别是A和B，把线段AB绕点A顺时针旋转90°得
线段AB＇.
⑴ 在图中画出△ABB＇，并直接写出点A和点B＇
的坐标；
⑵ 求直线AB＇表示的函数关系式；
⑶ 若动点C（1，a）使得S_△ABC=S_△ABB＇，
求a的值.

⑴画图基本准确.                ………………………………………………1分
点A（2，0）、点B＇(3，2) .                     ………………………3分
⑵把点A、点B＇的坐标分别代入y =kx+b，
得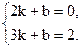
解得k=2，b= -4.
∴直线AB＇表示的函数关系式是y =2x-4 .                 ………………§K]
⑶∵△ABB＇为等腰直角三角形，直角边AB==，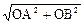
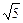∴ S_△_ABB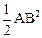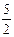_＇==.                  ……………………………………5分
在y =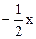+1中，当x=1时，y=0.5.
即直线x=1与AB交于点M（1，0.5）.
又∵点A和B到CM的距离之和显然为2，
∴ S_△_ABC=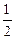CM×2= |a-0.5|=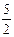.           …………………………………6分
解得，a=3，或-2.

解析

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

已知，如图，直线y=

与x轴、y轴分别交于A、B两点，⊙M经过

原点O及A、B两点．
（1）求以OA、OB两线段长为根的一元二方程；
（2）C是⊙M上一点，连接BC交OA于点D，若∠COD=∠CBO，写出经过O、C、A三点的二次函数的解析式；
（3）若延长BC到E，使DE=2，连接EA，试判断直线EA与⊙M的位置关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

（2002•岳阳）已知：如图，直线MN和⊙O切于点C，AB是⊙O的直径，AE⊥MN，BF⊥MN且与⊙O

交于点G，垂足分别是E、F，AC是⊙O的弦，
（1）求证：AB=AE+BF；
（2）令AE=m，EF=n，BF=p，证明：n²=4mp；
（3）设⊙O的半径为5，AC=6，求以AE、BF的长为根的一元二次方程；
（4）将直线MN向上平行移动至与⊙O相交时，m、n、p之间有什么关系？向下平行移动至与⊙O相离时，m、n、p之间又有什么关系？

查看答案和解析>>

科目：初中数学 来源： 题型：