练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．

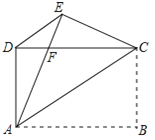
    （1）求证：△DEC≌△EDA；

    （2）求DF的值；

    【答案】见解析

    【解析】

    试题（1）由矩形和翻折的性质可知AD=CE，DC=EA，根据“SSS”可求得△DEC≌△EDA；

    （2）根据勾股定理即可求得

    试题解析：（1）由矩形的性质可知△ADC≌△CEA，

    ∴AD=CE，DC=EA，∠ACD=∠CAE，

    在△ADE与△CED中

    ∴△DEC≌△EDA（SSS）；

    （2）∵∠ACD=∠CAE，

    ∴AF=CF，

    设DF=x，则AF=CF=4﹣x，

    在RT△ADF中，AD2+DF2=AF2，

    即32+x2=（4﹣x）2，

    解得；x=，

    即DF=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

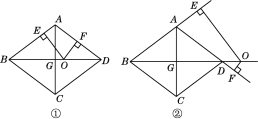
    【题目】如图，在边长为10的菱形ABCD中，对角线BD＝16，对角线AC，BD相交于点G，点O是直线BD上的动点，OE⊥AB于E，OF⊥AD于F.

    (1)求对角线AC的长及菱形ABCD的面积．

    (2)如图①，当点O在对角线BD上运动时，OE＋OF的值是否发生变化？请说明理由．

    (3)如图②，当点O在对角线BD的延长线上时，OE＋OF的值是否发生变化？若不变，请说明理由；若变化，请探究OE，OF之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两家商场平时以同样价格出售相同的商品，春节期间两家商场都让利酬宾，其中甲商场所有商品按8折出售，乙商场对一次购物中超过200元后的价格部分打7折．
    （1）以x（单位：元）表示商品原价，y（单位：元）表示购物金额，分别就两家商场的让利方式写出y关于x的函数解析式；
    （2）在同一直角坐标系中画出（1）中函数的图象；
    （3）春节期间如何选择这两家商场去购物更省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】开通了，中国联通公布了资费标准，其中包月元时，超出部分国内拨打元/分．由于业务多，小明的爸爸打电话已超出了包月费．下表是超出部分国内拨打的收费标准．

    时间/分

    1

    2

    3

    4

    5

    …

    电话费/元

    0.36

    0.72

    1.08

    1.44

    1.80

    …

    （1）这个表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

    （2）如果用表示超出时间，表示超出部分的电话费，那么与的关系式是什么？

    （3）如果打电话超出分钟，需多付多少电话费？

    （4）某次打电话的费用超出部分是元，那么小明的爸爸打电话超出几分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“阅读素养的培养是构建核心素养的重要基础，重庆十一中学校以‘大阅读’特色课程实施为突破口，着力提升学生的核心素养．”全校师生积极响应和配合，开展各种活动丰富其课余生活．在数学兴趣小组中，同学们从书上认识了很多有趣的数．其中有一个“和平数”引起了同学们的兴趣．描述如下：一个四位数，记千位上和百位上的数字之和为x，十位上和个位上的数字之和为y，如果，那么称这个四位数为“和平数”．

    例如：1423，，，因为，所以1423是“和平数”．

    （1）直接写出：最小的“和平数”是________，最大的“和平数”是__________；

    （2）求同时满足下列条件的所有“和平数”：

    ①个位上的数字是千位上的数字的两倍；

    ②百位上的数字与十位上的数字之和是12的倍数；

    （3）将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后这两个“和平数”为“相关和平数”．

    例如：1423于4132为“相关和平数”

    求证：任意的两个“相关和平数”之和是1111的倍数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为方便市民通行，某广场计划对坡角为30°，坡长为60 米的斜坡AB进行改造，在斜坡中点D 处挖去部分坡体（阴影表示），修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE．

    （1）若修建的斜坡BE 的坡角为36°，则平台DE的长约为多少米？

    （2）在距离坡角A点27米远的G处是商场主楼，小明在D点测得主楼顶部H 的仰角为30°，那么主楼GH高约为多少米？

    （结果取整数，参考数据：sin 36°＝0．6，cos 36°＝0．8，tan 36°＝0．7，＝1．7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是等边三角形，，点是边上一点，点是线段上点，连接、．当，时，________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形中，，，点是射线上一动点，以为边向右侧作等边，点的位置随着点的位置变化而变化．

    （1）如图1，当点在四边形内部或边上时，连接，与的数量关系是________，与的位置关系是_______；

    （2）如图2，当点在四边形外部时，（1）中的结论是否还成立？若成立，请予以证明；

    （3）如图3，当点在线段的延长线上时，连接，若，，则线段______，________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已如直线∥，且与、分别交于A、B两点，与、分别交于C、D两点，记∠ACP=∠1，∠BDP=∠2，∠CPD=∠3，点P在线段AB上.

    (1)若∠1=25°，∠2=33°，则∠3=__________；

    (2)猜想∠1，∠2，∠3之间的相等关系，并说明理由；

    (3)如图2，点在点B的南偏东23°方向，在点C的西南方向，利用(2)的结论，可知∠BAC=__________；

    (4)点P在直线上且在A、B两点外侧运动时，其它条件不变，请直接写出∠1，∠2，∠3之间的相等关系.

    查看答案和解析>>

    同步练习册答案