
 如图是屋顶的“人字形“钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为中柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=5m.
如图是屋顶的“人字形“钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为中柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=5m. 分析 先根据等腰三角形的性质及三角形内角和定理求出∠B=∠C=30°,根据直角三角形30°角所对的直角边等于斜边的一半得到DE=$\frac{1}{2}$BD,DF=$\frac{1}{2}$DC,两式相加,即可证明DE+DF=$\frac{1}{2}$BC.
解答 解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=$\frac{1}{2}$BD,DF=$\frac{1}{2}$DC,
∴DE+DF=$\frac{1}{2}$BD+$\frac{1}{2}$DC=$\frac{1}{2}$(BD+DC)$\frac{1}{2}$BC.
∴DE+DF=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5cm.
故答案为:5.
点评 此题主要考查等腰三角形的性质,三角形内角和定理及含30度角的直角三角形的性质的综合运用,用到的知识点为:等边对等角;三角形内角和为180°;直角三角形中,30°所对的直角边等于斜边的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 为饲养家禽需要围建两间同样大小的长方形禽舍,一边利用旧墙(如图),可供建造的围墙材料为24米,怎样设计,才能使两间禽舍的总面积最大?最大总面积为多少平方米?
为饲养家禽需要围建两间同样大小的长方形禽舍,一边利用旧墙(如图),可供建造的围墙材料为24米,怎样设计,才能使两间禽舍的总面积最大?最大总面积为多少平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
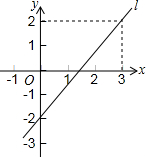 如图所示,直线l是一次函数y=kx+b在直角坐标系内的图象.
如图所示,直线l是一次函数y=kx+b在直角坐标系内的图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com