分析:①根据公式
=|a|把所求式子化简,然后由x的范围判定出2-x为负数,根据负数的绝对值等于它的相反数即可得到化简结果,作出判断;
②满足题意的圆内接多边形还可以为邻边不等的矩形,不一定是正方形,本选项错误;
③解不等式mx>1,需在不等式两边同时除以m,根据解集可知不等号方向改变,故得到m为负数,本选项正确;
④根据题意画出图形,利用同角的余角相等得到三角形ACD与三角形BCD有一对锐角相等,再加上一对直角相等,根据两对对应角相等,可得两三角形相似,由相似得比例即可得证.
解答:解:①当x≥2时,得到2-x≤0,
所以
=|2-x|=-(2-x)=x-2,本选项正确;
②各角相等的圆内接多边形可以为邻边不等的矩形,不一定为正方形,本选项错误;
③解不等式mx>1时,应在不等式两边同时除以m,根据解集x<
得到不等号方向改变,故m<0,本选项正确;
④根据题意画出图形,如图所示:
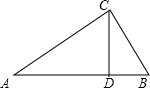
∵CD⊥AB,∴∠CDA=∠CDB=90°,
∴∠A+∠ACD=90°,
又∠ACB=90°,∴∠A+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴
=
,即CD
2=AD•DB,本选项正确,
则说法正确序号有①③④,共3个.
故选B
点评:此题考查了二次根式的化简,相似三角形的判定与性质,以及不等式的基本性质,要求学生掌握公式
=|a|及绝对值的代数意义;不等式基本性质3:在不等式两边同时乘以或除以同一个负数时,不等号方向要改变,要求学生理解说明一个命题是假命题只需要举一个反例即可;要说明一个命题是真命题,必须经过严格的证明.学生建立良好的知识结构体系是解本题的关键.




 阅读快车系列答案
阅读快车系列答案