
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

【答案】(1)∠F=30°;(2)DF=6.
【解析】
(1)、根据等边三角形的性质得出∠B=60°,根据DE∥AB得出∠EDC=60°,根据垂直得出∠DEF=90°,根据三角形内角和定理可得∠F的度数;
(2)、根据∠ACB=∠EDC=60°得出△EDC为等边三角形,则ED=DC=3,根据∠DEF=90°,∠F=30°得出DF=2DE=6.
(1)∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=3,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=6.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的切线;
(2)若⊙O的半径为5,sinF=![]() ,求DF的长。
,求DF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A、B分别表示的数是![]() 、
、![]() ,记A、B两点间的距离为AB
,记A、B两点间的距离为AB
(1) 若a=6,b=4,则AB= ;若a=-6,b=4,则AB= ;
(2) 若A、B两点间的距离记为![]() ,试问
,试问![]() 和
和![]() 、
、![]() 有何数量关系?
有何数量关系?
(3)写出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和.
(4)|x-1|+|x+2|取得的值最小为 ,|x-1|-|x+2|取得最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的表达式为
的表达式为![]() ,直线
,直线![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() :
:![]() 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线![]() 、
、![]() 交于点
交于点![]() .
.
(1)求m的值;
(2)求直线![]() 的表达式;
的表达式;
(3)根据图象,直接写出![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.邮箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.

(1)汽车行驶 h后加油,加油量为 L;
(2)求加油前油箱剩余油量Q与行驶时间t之间的函数关系式;
(3)如果加油站离目的地还有200km,车速为40km/h,请直接写出汽车到达目的地时,油箱中还有多少汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魔术大师夏尔![]() 巴比耶90岁时定义了一个魔法三角阵,三角阵中含有四个区域(三个“边区域”和一个“核心区域”,如图1中的阴影部分),每个区域都含有5个数,把差相同的连续九个正整数填进三角阵中,每个区域的5个数的和必须相同。例如:图2中,把相差为1的九个数(1至9)填入后,三个“边区域”及“核心区域”的数的和都是22,即6+1+9+2+4=22,4+2+8+3+5=22,5+3+7+1+6=22,2+9+1+7+3=22
巴比耶90岁时定义了一个魔法三角阵,三角阵中含有四个区域(三个“边区域”和一个“核心区域”,如图1中的阴影部分),每个区域都含有5个数,把差相同的连续九个正整数填进三角阵中,每个区域的5个数的和必须相同。例如:图2中,把相差为1的九个数(1至9)填入后,三个“边区域”及“核心区域”的数的和都是22,即6+1+9+2+4=22,4+2+8+3+5=22,5+3+7+1+6=22,2+9+1+7+3=22

(1)操作与发现:
在图3中,小明把差为1的连续九个正整数(1至9)分为三组,其中1、2、3为同一组,4、5、6为同一组,7、8、9为同一组,把同组数填进同一花纹的△中,生成了一个符合定义的魔法三角阵,且各区域的5个数的和为28,请你在图3中把小明的发现填写完整.

(2)操作与应用:
根据(1)发现的结果,把差为8的连续九个正整数填进图4中,仍能得到符合定义的魔法三角阵,且各区域的5个数的和为2019.
①设其中最小的数为![]() ,则最大的数是_________;(用含
,则最大的数是_________;(用含![]() 的式子表示).
的式子表示).
②把图4中的9个数填写完整,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
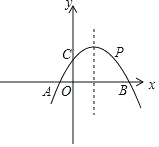
【题目】如图,已知抛物线y=ax2+bx+1与x轴分别交于A(﹣1,0),B(3,0),与y轴交于点C.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上有点P,使△PBC面积为1,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com