
在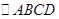 中,对角线
中,对角线 为BD延长线上一点且
为BD延长线上一点且 为等边三角形,
为等边三角形, 、
、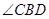 的平分线相交于点
的平分线相交于点 ,连接
,连接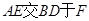 ,连接
,连接 。
。

(1)若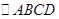 的面积为
的面积为 ,求
,求 的长;
的长;
(2)求证: 。
。
(1)AG=6 (2)要证明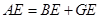 ,则可通过证明
,则可通过证明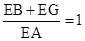 即可。
即可。
【解析】
试题分析:(1)解∵四边形ABCD为平行四边形,所以AD∥BC。∵BC⊥DB,∴AD⊥BD。
∵△AGB为等边三角形,∴AG=AB=BG=8.所以DG=DB=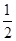 BG=4(三线合一定理)
BG=4(三线合一定理)
在Rt△ADB中,S△ADB=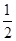 AD×BD=
AD×BD=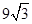 。设BD=x,则AD=
。设BD=x,则AD=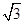 x。则
x。则
所以AG=6
(2)证明:因为△ABG为等边三角形,所以∠GBA=∠GAB=∠ABG=60°。
∵BD⊥AD。所以∠BAD=30°。因为EA是∠BAD角平分线,∠CBD=90°。
∴∠BAE =∠DAE=15°。因为BE为∠CBD平分线,∠CBD=90°,
所以∠EBD=45°。∠EBA=45°+60°=105°。
则∠BEA=180°-105°-15°=60°。所以∠BEA=∠FBA,∠BFE=∠GFC,
∴△AFB∽△ABE
∴ ∵∠GAE=60°-15°=45°=∠EBF,∠BFE=∠GFA,
∵∠GAE=60°-15°=45°=∠EBF,∠BFE=∠GFA,
∴△BFE∽△AFG,∴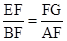
∵∠EFG=∠BFA,∴△EFG∽△BFA
∴∠GEF=∠ABF=60°。而∠BGA=60°。所以△AGF∽△CEG
∴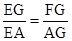 所以
所以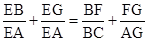
因为△BAG为等边三角形,所以BA=AG=BG=BF+FG
所以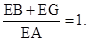 所以AE=BE+GE
所以AE=BE+GE
考点:特殊三角形性质喝平行四边形性质
点评:本题考查了平行四边形性质,勾股定理,等腰三角形的性质,等边三角形的性质,三角形的内角和定理,相似三角形的性质和判定等知识点的综合运用,本题综合性比较强,难度偏大.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
 在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.若平行四边形ABCD的面积为9
在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.若平行四边形ABCD的面积为9| 3 |
查看答案和解析>>
科目:初中数学 来源:2013届重庆市万州区岩口复兴学校九年级下学期第一次(3月)月考数学卷(带解析) 题型:解答题
在 中,对角线
中,对角线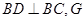 为BD延长线上一点且
为BD延长线上一点且 为等边三角形,
为等边三角形,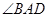 、
、 的平分线相交于点
的平分线相交于点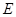 ,连接
,连接 ,连接
,连接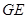 。
。
(1)若 的面积为
的面积为 ,求
,求 的长;
的长;
(2)求证: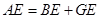 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
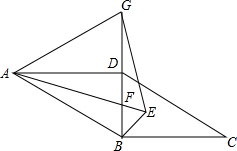 在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.若平行四边形ABCD的面积为
在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.若平行四边形ABCD的面积为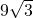 ,求AG的长.
,求AG的长.查看答案和解析>>
科目:初中数学 来源:2012年云南省中考数学模拟试卷(四)(解析版) 题型:解答题
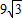 ,求AG的长.
,求AG的长.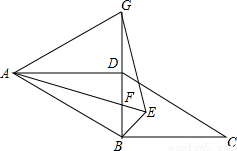
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com