
【题目】阅读下面文字:
对于(﹣5![]() )+(﹣9
)+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
可以如下计算:
原式=[(﹣5)+(﹣![]() )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣![]() )]+(17+
)]+(17+![]() )+[(﹣3)+(﹣
)+[(﹣3)+(﹣![]() )]
)]
=[(一5)+(﹣9)+17+(一3)]+[(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() +(﹣
+(﹣![]() )]=0+(﹣1
)]=0+(﹣1![]() )
)
=﹣1![]()
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1![]() )+(﹣2000
)+(﹣2000![]() )+4000
)+4000![]() +(﹣1999
+(﹣1999![]() )
)
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
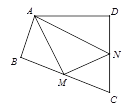
【题目】四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,有一根木棒MN放置在数轴上,它的两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5.(单位:cm)则木棒MN长为__________cm.

(2)一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你借助上述方法,写出小民爷爷到底是_________岁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

查看答案和解析>>
科目:初中数学 来源: 题型:
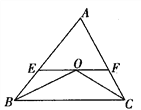
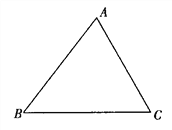
【题目】已知:如图,∠ABC和∠ACB的平分线交于点O,EF经过点O且平行于BC,分别与AB,AC交于点E,F.
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)若∠ABC=,∠ACB=,用,的代数式表示∠BOC的度数.
(3)在第(2)问的条件下,若∠ABC和∠ACB邻补角的平分线交于点O,其他条件不变,请画出相应图形,并用,的代数式表示∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
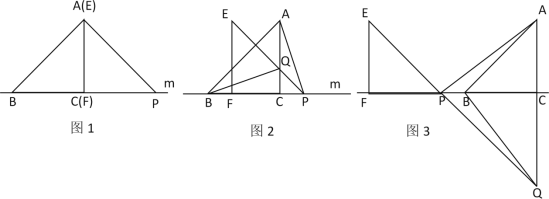
【题目】(1)问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,
在图1中,AB与AP的数量关系是_______,AB与AP的位置关系是_______
(2)操作发现:将△EFP沿直线m向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并证明BQ与AP的数量关系和位置关系
(3)猜想论证:将△EFP沿直线m向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,(2)中的结论还成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
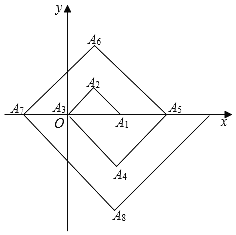
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6.…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0).则依图中所示规律,A2020的坐标为( )
A.(2,﹣1010)B.(2,﹣1008)C.(1010,0)D.(1,1009)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com