
分析 (1)利用平方差公式和完全平方公式展开后合并即可得;
(2)将x、y的值代入原式=(x+y)2-xy,利用平方差公式和完全平方公式计算可得.
解答 解:(1)原式=2-3+8+12$\sqrt{6}$+27=34+12$\sqrt{6}$;
(2)当x=$\sqrt{3}$+1,y=$\sqrt{3}$-1时,
原式=(x+y)2-xy.
=($\sqrt{3}$+1+$\sqrt{3}$-1)2-($\sqrt{3}$+1)($\sqrt{3}$-1)
=12-(3-1)
=10.
点评 本题主要考查二次根式的化简求值和完全平方公式及平方差公式的运用,熟练掌握平方差公式和完全平方公式的变形及二次根式的性质是解题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$x2+1 | B. | y=$\frac{1}{2}$x2-1 | C. | y=$\frac{1}{2}$(x+1)2 | D. | y=$\frac{1}{2}$(x-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 矩形面积固定,长x和宽y的关系 | B. | 矩形周长固定,长x和宽y的关系 | ||
| C. | 正方形面积S和边长a之间的关系 | D. | 正方形周长C和边长a之间的关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
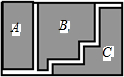 如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.
如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com