
分析 根据车头进入隧道到车尾离开隧道共需2.43分钟和整辆货车全在隧道的时间为2.406分钟表示出货车的速度,根据速度不变列方程即可.
解答 解:根据题意,得
车头进入隧道到车尾离开隧道共需2.43分钟,则其速度是$\frac{x+16}{2.43}$,
整辆货车完全在隧道的时间为2.406分钟,则其速度是$\frac{x-16}{2.406}$.
则有方程:$\frac{x+16}{2.43}$=$\frac{x-16}{2.406}$.
故答案为$\frac{x+16}{2.43}$=$\frac{x-16}{2.406}$.
点评 本题考查了由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:选择题
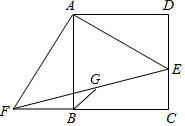 E为正方形ABCD的边CD上一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:①G在△ABF的外接圆上;②EC=$\sqrt{2}$BG;③B,G,D三点在同一条直线上;④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD,那么E为DC的黄金分割点.正确的是( )
E为正方形ABCD的边CD上一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:①G在△ABF的外接圆上;②EC=$\sqrt{2}$BG;③B,G,D三点在同一条直线上;④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD,那么E为DC的黄金分割点.正确的是( )| A. | ①② | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
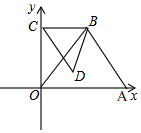 如图,直角坐标系中,O为原点,A(6,0),在等腰三角形ABO中,OB=BA=5,点B在第一象限,C(0,k)为y轴正半轴上一动点,作以∠CBD为顶角的等腰三角形CBD,且∠CBD=∠OBA,连结AD.
如图,直角坐标系中,O为原点,A(6,0),在等腰三角形ABO中,OB=BA=5,点B在第一象限,C(0,k)为y轴正半轴上一动点,作以∠CBD为顶角的等腰三角形CBD,且∠CBD=∠OBA,连结AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
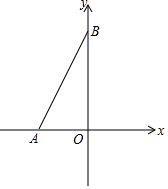 在平面直角坐标系中,A(a,0),B(0,b),且a、b是二元一次方程组$\left\{\begin{array}{l}{a+b-4=0}\\{\frac{1}{2}a-2b+13=0}\end{array}\right.$的解.
在平面直角坐标系中,A(a,0),B(0,b),且a、b是二元一次方程组$\left\{\begin{array}{l}{a+b-4=0}\\{\frac{1}{2}a-2b+13=0}\end{array}\right.$的解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线a经过点A(0,1)且垂直于y轴,直线b经过点B(2,0)且垂直于x轴,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与直线a,b分别交于点E、D.
如图,直线a经过点A(0,1)且垂直于y轴,直线b经过点B(2,0)且垂直于x轴,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与直线a,b分别交于点E、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{4}(x+2)^{2}+2$ | B. | y=$\frac{1}{4}$(x-2)2-2 | C. | y=$\frac{1}{4}$(x+2)2-2 | D. | y=$\frac{1}{4}$(x-2)2+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com