
【题目】设点A(x1,y1)和点B(x2,y2)是反比例函数y=![]() 图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
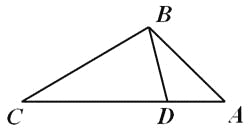
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了解同学们对金庸武侠小说的阅读情况,随机对初三年级的部分同学进行调查,将调查结果分成以下五类:A:看过0~3本,B:看过4~6本,C:看过7~9本,D:看过10~12本,E:看过13~15本.并根据调查结果绘制了如图1、图2两幅不完整的统计图.
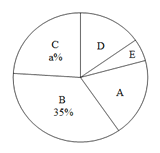
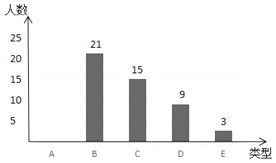
(1)图2中的a = ,D所对的圆心角度数为 °;
(2)请补全条形统计图;
(3)本次调查中E类有2男1女,王老师想从中抽取2名同学分别撰写一篇读书笔记.请用列表或画树状图的方法求所抽取的两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
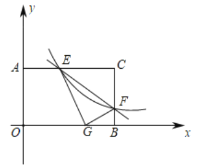
【题目】在矩形![]() 中,分别以
中,分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.![]() 是
是![]() 边上一个动点(不与
边上一个动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 的反比例函数
的反比例函数![]()
![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,则
处,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 郑州外国语中学为了解学生课下阅读所用时间的情况,从各年级学生中随机抽查了一部分学生进行统计,下面是针对此次统计所制作的不完整的频数分布表和频数分布直方图,请根据图表信息回答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |
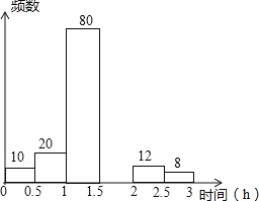
(1)表中a=______b=______;
(2)请补全频数分布直方图;
(3)样本中,学生日阅读所用时间的中位数落在第______组;
(4)该校共有学生3000人,请估计学生日阅读量不少于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钝角△ABC中,AB=AC,BC=2![]() ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1的坐标为(0,1),点A2在x轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,交y轴于点A3;过点A3作A3A4⊥A2A3,交x轴于点A4;过点A4作A4A5⊥A3A4,交y轴于点A5;……;按此规律进行下去,则点A2021的坐标为( )
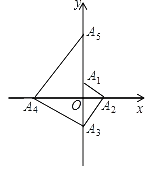
A.(0,31011)B.(﹣31011,0)C.(0,31010)D.(﹣31010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有专家指出:人为型空气污染(如汽车尾气排放等)是雾霾天气的重要成因.某校为倡议“每人少开一天车,共建绿色家园”,想了解学生上学的交通方式.九年级(8)班的5名同学联合设计了一份调查问卷.对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,扇形统计图中“骑自行车”所在扇形的圆心角度数是 度,请补全条形统计图;
(2)已知这5名学生中有2名女同学,要从这5名学生中任选两名同学汇报调查结果.请用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
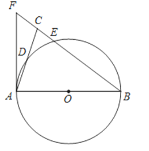
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com