
如图2,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )

图2
A.10° B.15° C.20° D.25°
科目:初中数学 来源: 题型:
给出下列命题:①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三角形的角平分线是射线 ④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外 ⑤任何一个三角形都有三条高、三条中线、三条角平分线
⑥三角形的三条角平分线交于一点,且这点在三角形内。正确的命题有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图6,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A. 30,2 B.60,2 C.60, D.60,
D.60,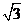

图6
查看答案和解析>>
科目:初中数学 来源: 题型:
如图12,在平面直角坐标系中,三角形②③是由三角形①依次旋转后所得的图形.
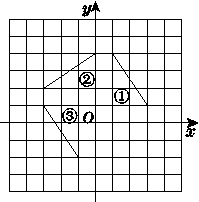
图12
(1)在图中标出旋转中心P的位置,并写出它的坐标;
(2)在图中画出再次旋转后的三角形④.
查看答案和解析>>
科目:初中数学 来源: 题型:
勾股定理是几何中的一个重要定理, 在我国古算书《周髀算经》中就有“若勾三,股四,则弦五
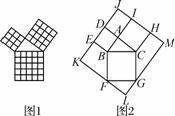
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五 ”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.90 B.100 C.110 D.121
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com