
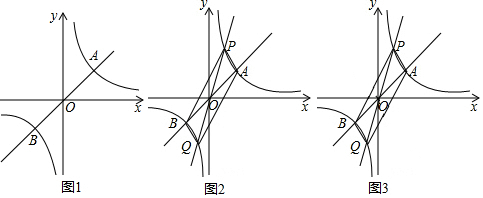
分析 (1)利用A点坐标可分别求得双曲线和直线的解析式,联立两函数解析式则可求得B点坐标,从而可求得OA和OB的长,可求得答案;
(2)①联立双曲线和直线PQ的解析式,可表示出P、Q的坐标,可求得OP=OQ,则可证得结论;②由双曲线和两直线解析式可分别求得A、B、P、Q的坐标,可求得OA=OB、OP=OQ,则可证得四边形APBQ为平行四边形.
解答 解:
(1)∵双曲线y=$\frac{k}{x}$(k>0)与直线y=k1x交于A,B两点,且A(4,2),
∴2=$\frac{k}{4}$,2=4k1,解得k=8,k1=$\frac{1}{2}$,
∴双曲线解析式为y=$\frac{8}{x}$,直线AB解析式为y=$\frac{1}{2}$x,
联立两函数解析式可得$\left\{\begin{array}{l}{y=\frac{8}{x}}\\{y=\frac{1}{2}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$,
∴B(-4,-2),
∴A、B关于原点对称,
∴OA=OB,
故答案为:(-4,-2);=;
(2)①联立双曲线与直线PQ解析式可得$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y={k}_{2}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{\sqrt{k{k}_{2}}}{{k}_{2}}}\\{y=\sqrt{k{k}_{2}}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{\sqrt{k{k}_{2}}}{{k}_{2}}}\\{y=-\sqrt{k{k}_{2}}}\end{array}\right.$,
∴P($\frac{\sqrt{k{k}_{2}}}{{k}_{2}}$,$\sqrt{k{k}_{2}}$),Q(-$\frac{\sqrt{k{k}_{2}}}{{k}_{2}}$,-$\sqrt{k{k}_{2}}$),即P、Q关于原点对称,
∴OP=OQ,
由(1)可得OA=OB,
∴四边形APBQ一定是平行四边形;
②四边形APBQ为矩形.,理由如下:
当k=12,k1=$\frac{3}{4}$,k2=$\frac{4}{3}$时,
双曲线解析式为y=$\frac{12}{x}$,直线AB解析式为y=$\frac{3}{4}$x,直线PQ解析式为y=$\frac{4}{3}$x,
联立双曲线和直线AB解析式可得$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=\frac{3}{4}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-3}\end{array}\right.$,
∴A(4,3),B(-4,-3),
∴OA=OB=5,
同理可求得P(3,4),Q(-3,-4),
∴OP=OQ=5,
∴OA=OB=OP=OQ,
∴四边形APBQ为矩形.
点评 本题为反比例函数的综合应用,涉及函数图象的交点、待定系数法、中心对称的性质、平行四边形的判定、矩形的判定等知识.在(1)中求得双曲线与直线AB的解析式是解题的关键,在(2)①中表示出P、Q的坐标是解题的关键,在(2)②中求得A、B、P、Q的坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
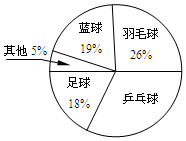 闵行区某校对六年级新生第一学期体育选修课的情况作了全面调查.结果如图.根据如图解答下列问题:
闵行区某校对六年级新生第一学期体育选修课的情况作了全面调查.结果如图.根据如图解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
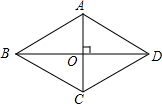 如图,四边形ABCD是对角线互相垂直的四边形,且AB=BC,请你添加一个适当的条件AB=AD,使四边形ABCD成为菱形.(只需添加一个即可).
如图,四边形ABCD是对角线互相垂直的四边形,且AB=BC,请你添加一个适当的条件AB=AD,使四边形ABCD成为菱形.(只需添加一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2a3•3a2=-6a5 | B. | 3a2•4a2=12a2 | C. | (a+1)(a-1)=a2-a+1 | D. | a15÷a3=a5(a≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)(a+c)=a2-ab+ac+bc | B. | x2•x3=x6 | ||
| C. | (x-2)2=x2-42 | D. | 5-1=$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com