练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    反比例函数在第二象限的图象如图所示.
    （1）直接写出m的取值范围；
    （2）若一次函数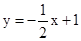的图象与上述反比例函数图象交于点A，与x轴交于点B，△AOB的面积为，求m的值.

    （1）m＜-1；（2）.

    解析试题分析：（1）根据反比例函数的图象和性质得出m+1＜0，求出即可.
    （2）求出B的坐标，求出OB边上的高，得出A的纵坐标，代入一次函数的解析式，求出A的横坐标，把A的坐标代入反比例函数解析式求出即可．
    试题解析：（1）∵反比例函数的图象在第二象限，
    ∴m+1＜0，
    ∴m＜-1.
    （2）令，则，解得到，∴ .∴OB=2.
    ∵，∴ ，解得.
    ∵点A在直线上，∴，解得. ∴.
    ∴，解得 .
    考点：反比例函数与一次函数的交点问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    一辆轿车从甲地驶往乙地，到达乙地后返回甲地，速度是原来的1.5倍，共用t小时；一辆货车同时从甲地驶往乙地，到达乙地后停止．两车同时出发，匀速行驶．设轿车行驶的时间为x（h），两车到甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图．
    （1）求轿车从乙地返回甲地时的速度和t的值；
    （2）求轿车从乙地返回甲地时y与x之间的函数关系式，并写出自变量x的取值范围；
    （3）直接写出轿车从乙地返回甲地时与货车相遇的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    直线y=﹣x+6与坐标轴分别交于A、B两点，动点P、Q同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动．
    （1）直接写出A、B两点的坐标；
    （2）设点Q的运动时间为t（秒），△OPQ的面积为S，求出S与t之间的函数关系式；
    （3）当S=时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线y=mx与双曲线y=相交于A、B两点，A点的坐标为（1，2）
    （1）求反比例函数的表达式；
    （2）根据图象直接写出当mx＞时，x的取值范围；
    （3）计算线段AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数的图象交于一、三象限的A、B两点，与x轴交于点C．已知，，．    
    （1）求反比例函数和一次函数的解析式；
    （2）求△OBC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    快、慢两车分别从相距360千米路程的甲、乙两地同时出发，匀速行驶，先相向而行，快车到达乙地后，停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地，快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示．

    请结合图象信息解答下列问题：
    (1)慢车的速度是     千米／小时，快车的速度是     千米／小时；
    (2)求m的值，并指出点C的实际意义是什么？
    (3)在快车按原路原速返回的过程中，快、慢两车相距的路程为150千米时，慢车行驶了多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，⊙M与x轴相切于点C，与y轴的一个交点为A。
    （1）求证：AC平分∠OAM；
    （2）如果⊙M的半径等于4，∠ACO=300，求AM所在直线的解析式．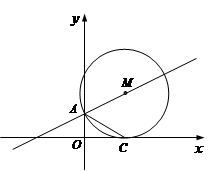

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知反比例函数（x > 0，k是常数）的图象经过点A（1,4），点B（m , n），其中m＞1， AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．
    （1）写出反比例函数解析式；
    （2）求证：∆ACB∽∆NOM；
    （3）若∆ACB与∆NOM的相似比为2，求出B点的坐标及AB所在直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人距B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
    （1）写出A、B两地之间的距离；
    （2）求出点M的坐标，并解释该点坐标所表示的实际意义；
    （3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．

    查看答案和解析>>

    同步练习册答案