
 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿折线BC-CD做匀速运动,则△APB的面积S与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿折线BC-CD做匀速运动,则△APB的面积S与点P运动的路程x之间的函数图象大致是( )| A. | 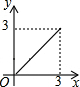 | B. |  | C. |  | D. |  |
分析 运用动点函数进行分段分析,当P在BC上与CD上时,分别求出函数解析式,再结合图象得出符合要求的解析式.
解答 解:∵AB=2,BC=1,动点P从点B出发,P点在BC上时,BP=x,AB=2,
∴△ABP的面积S=$\frac{1}{2}$×AB×BP=$\frac{1}{2}$×2x=x;
动点P从点B出发,P点在CD上时,△ABP的高是1,底边是2,所以面积是1,即s=1;
∴s=x时是正比例函数,且y随x的增大而增大,
s=1时,是一个常数函数,是一条平行于x轴的直线.
所以只有B符合要求.
故选B.
点评 此题主要考查了动点函数的应用,注意将函数分段分析得出解析式是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 6a2b2=3ab•2ab | B. | 2x2+8x-1=2x(x+4)-1 | ||
| C. | a2-3a-4=(a+1)(a-4) | D. | a2-1=a(a-$\frac{1}{a}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连结BH并延长并CD于点F,连结DE交BF于点O,下列结论:
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连结BH并延长并CD于点F,连结DE交BF于点O,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com