
如图:在▱ABCD中,AC为 其对角线,过点D作AC的平行线与BC的延长线交于E.
其对角线,过点D作AC的平行线与BC的延长线交于E.
(1)求证:△ABC≌△DCE;
(2)若AC=BC,求证:四边形ACED为菱形.

科目:初中数学 来源: 题型:
如图①是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,则折痕DE的长为( )
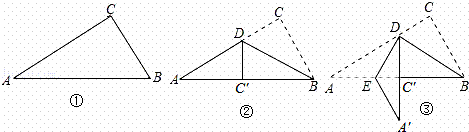
A. 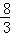 cm B.2
cm B.2 cm C.2
cm C.2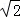 cm D. 3cm
cm D. 3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
已知甲校有a人,其中男生占60%;乙校有b人,其中男生占50%.今将甲、乙两校合并后,小清认为:「因为 =55%,所以合并后的男生占总人数的55%.」如果是你,你会怎么列式求出合并后男生在总人数中占的百分比?你认为小清的答案在任何情况都对吗?请指出你认为小清的答案会对的情况.请依据你的列式检验你指出的情况下小清的答案会对的理由.
=55%,所以合并后的男生占总人数的55%.」如果是你,你会怎么列式求出合并后男生在总人数中占的百分比?你认为小清的答案在任何情况都对吗?请指出你认为小清的答案会对的情况.请依据你的列式检验你指出的情况下小清的答案会对的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
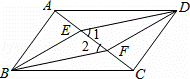
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,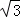 =1.73);
=1.73);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com