
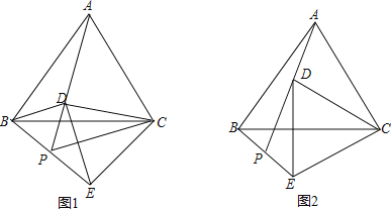
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
【答案】(1)①△BCE;②60°;(2)PD+PE=PC,证明见解析;(3)CE的最大值为6.
【解析】
(1)①根据旋转的性质和等边三角形的性质以及全等三角形的判定证明即可;
②根据全等三角形的判定和性质以及三角形内角和解答即可;
(2)根据等边三角形的性质以及全等三角形的判定和性质解答即可;
(3)由(1)可得CE=CD,根据D点在线段AC上,CD长度最小;D点在CA的延长线上,CD的长度最大,求出CD的最大值即可求得线段CE的最大值.
(1)①如图1中,
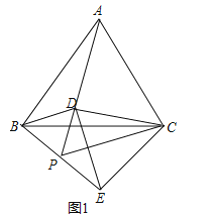
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,
∵将线段CD绕C顺时针旋转60°得到线段CE,
∴CE=CD,∠DCE=60°,
∴△DCE是等边三角形,
∴∠DCE═60°,
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS).
故答案为:△BCE.
②∵△ACD≌△BCE,
∴∠EBC=∠DAC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠PBC+∠BAD=60°,
∴∠APB=180°-∠ABC+∠PBC+∠BAP=180°-60°-60°=60°;
故答案为:60°.
(2)结论:PD+PE=PC.
理由:∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠CAD+∠BAD=60°,∠BAD+∠DBC=60°,
∴∠BAD+∠ABD=∠BDP=60°,
∵∠APB=60°,
∴△BDP是等边三角形,
∴DP=BP,
∴PD+PE=BE,
∵△ADC≌△BEC,
∴AD=BE,
∵在△ABD与△CBP中
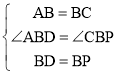 ,
,
∴△ABD≌△CBP(SAS),
∴AD=PC,
∴PD+PE=PC;
(3)如图2中,
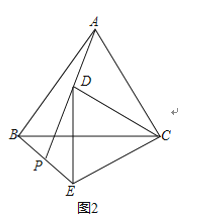
∵AC=4,AD=2,
∴D点在线段AC上,CD长度最小;D点在CA的延长线上,CD的长度最大,
∴4-2≤CD≤4+2,
∴2≤CD≤6.
∴CD的最大值为6,
由(1)可知△ACD≌△BCE,EC=CD,
∴EC的最大值为6.


科目:初中数学 来源: 题型:
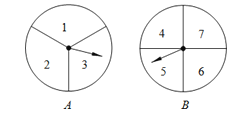
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
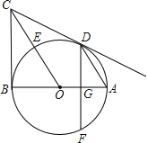
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若sin∠BAD=![]() ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
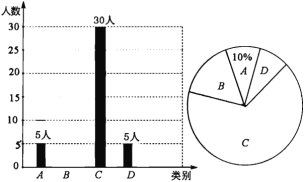
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察以下等式:
第1个等式:![]() ; 第2个等式:
; 第2个等式:![]() ;
;
第3个等式:![]() ;第4个等式:
;第4个等式:![]() ;…
;…
按照以上规律,解决下列问题:
(1)写出第5个等式:_______________
(2)写出你猜想的第n个等式:________________________(用含n的等式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨![]() 元(
元(![]() 为非负整数),每个月的销售利润为
为非负整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,AB=BD,点B、C、D、G四个点在同一个圆⊙O上,连接BG 并延长交AD于点F,连接DG并延长交AB于点E,BD与CG交于点H,连接FH,下列结 论:①AE=DF;②FH∥AB;③△DGH∽△BGE;④当CG为⊙O的直径时,DF=AF.其中正确结论的个数是( )
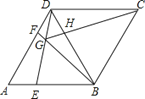
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com