
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=﹣1,经过点(0,1)有以下结论:①a+b+c<0;②b2﹣4ac>0;③abc>0;④4a﹣2b+c>0;⑤c﹣a>1.其中所有正确结论的序号是_____.
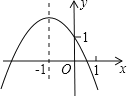
【答案】①②③④⑤.
【解析】
①根据![]() 对应的函数值即可判断①的正误;
对应的函数值即可判断①的正误;
②根据抛物线与x轴交点情况可判断②的正误;
③由对称轴的位置可判断ab的正负,由抛物线与y轴的交点判断c的正负,从而可判断③的正误;
④根据![]() 对应的函数值即可判断④的正误;
对应的函数值即可判断④的正误;
⑤根据c的值及a的正负即可判断⑤的正误.
解:① x=1时,y=a+b+c<0,正确,符合题意;
② 抛物线与x轴有2个交点,故b2﹣4ac>0正确,符合题意;
③ 对称轴在y轴左侧,则ab>0,而抛物线与y轴的交点为![]() ,所以c>0,故abc>0正确,符合题意;
,所以c>0,故abc>0正确,符合题意;
④ 由函数的对称性知,x=﹣2和x=0对称,故x=﹣2时,y=4a﹣2b+c=1>0,正确,符合题意;
⑤ 抛物线与y轴的交点为![]() ,所以c=1,抛物线开口向下,所以a<0,故c﹣a>1,正确,符合题意.
,所以c=1,抛物线开口向下,所以a<0,故c﹣a>1,正确,符合题意.
故答案为:① ② ③ ④ ⑤.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润![]() (单位:元)与售价
(单位:元)与售价![]() (单位:元/千克)之间的函数关系式.
(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是AB边的中点,点E为AC中点,点F在边BC上,AF交DE于点G,点H是FC的中点,连接GH.

(1)如图1,求证:四边形GHCE是平行四边形;
(2)如图2,当AB=AC,点F是BC中点时,在不添加任何辅助线的情况下,请直接写出图中所有长度等于![]() BF的线段.
BF的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是

A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图所示,某学生在河东岸点![]() 处观测到河对岸水边有一点
处观测到河对岸水边有一点![]() ,测得
,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达![]() 处,测得
处,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一组方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为
,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为![]() ;第②个方程的解为
;第②个方程的解为![]() ;第③个方程的解为
;第③个方程的解为![]() .若n为正整数,且关于x的方程
.若n为正整数,且关于x的方程![]() 的一个解是
的一个解是![]() ,则n的值等于____________.
,则n的值等于____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com