
【题目】综合题
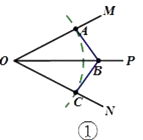
(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
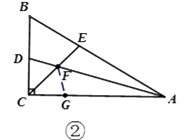
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
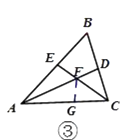
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.
【答案】
(1)解:如图①所示,△COB≌△AOB,点C即为所求.
(2)解:如图②,在CG上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
CG=CD,∠DCF=∠GCF,CF=CF,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC= ![]() ∠BAC,∠FCA=
∠BAC,∠FCA= ![]() ∠ACB,且∠EAF=∠GAF,
∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA= ![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)= ![]() =60°,
=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
∠AFE=∠AFG,AF=AF,∠EAF=∠GAF,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)解:DF=EF 仍然成立.
证明:如图③,在CG上截取AG=AE,
同(2)可得△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA.
又由题可知,∠FAC= ![]() ∠BAC,∠FCA=
∠BAC,∠FCA= ![]() ∠ACB,
∠ACB,
∴∠FAC+∠FCA= ![]() (∠BAC+∠ACB)=60°,
(∠BAC+∠ACB)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.
【解析】(1)以O为圆心,OA为半径画弧,交ON于点C,连接BC,利用边角边即可知道△COB≌△AOB。
(2)根据题意添加辅助线,在CG上截取CG=CD,根据角平分线的定义证出∠DCF=∠GCF,从而可证得△CFG≌△CFD,得出DF=GF。要证EF=FD,转化为证EF=GF,因此需证△AFG≌△AFE,根据图形及已知还需差一个条件。根据已知∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,易证得∠AFC=120°,即可得到∠AFE=∠AFG=60°,继而可证明△AFG≌△AFE,即可证得结论。
(3)通过分析,结论仍然成立,添加辅助线的方法和证明方法同(2)一样。
【考点精析】掌握角的平分线和三角形的内角和外角是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. 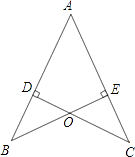
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“对于实数m,n,k,若m=n,n=k,则m=k”,即相等关系具有传递性.小敏由此进行联想,提出了下列命题:
①a,b,c是直线,若a∥b,b∥c,则a∥c.
②a,b,c是直线,若a⊥b,b⊥c,则a⊥c.
③若∠α与∠β互余,∠β与∠γ互余,则∠α与∠γ互余.
其中正确的命题是( )
A.①B.①②C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 的一组对边
的一组对边![]() 的延长线相交于点
的延长线相交于点![]() .
.

(1)如图1,若![]() ,求证
,求证![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为6,求四边形
的面积为6,求四边形![]() 的面积;
的面积;
(3)如图3,另一组对边![]() 的延长线相交于点
的延长线相交于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=3x的图象与反比例函数y= ![]() 的图象交于点A(1,m)和点B.
的图象交于点A(1,m)和点B.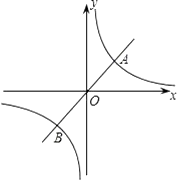
(1)求m的值和反比例函数的解析式.
(2)观察图象,直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com