
【题目】如图,矩形纸片ABCD,AB=![]() ,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
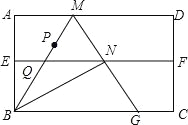
(1)求证:∠ABM=30°;
(2)求证:△BMG是等边三角形;
(3)若P为线段BM上一动点,求PN+PG的最小值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由对折,判断出BN垂直平分MG,通过计算即可;
(2)由(1)∠ABM=∠NBM=GBN=30°,得出∠MBG=60°,即可;
(3)先计算出BG=BM=2,再判断出点N与点A关于直线BM对称,得到PN+PG的最小值为AG,计算即可.
试题解析:(1)∵对折AD与BC重合,
∴点E是AB的中点,
∴点N是MG的中点,
∵∠BNM=∠A=90°,
∴BN垂直平分MG,
∴BM=BG,
∴∠GBN=∠MBN,
由翻折的性质,∠ABM=∠NBM,
∴∠ABM=∠NBM=∠GBN=![]() ×90°=30°,
×90°=30°,
∴∠MBG=60°;
(2)由(1)知,∠ABM=∠NBM=GBN=30°,
∴∠MBG=60°,
∵BM=BG,
∴△BMG为等边三角形,
(3)如图,
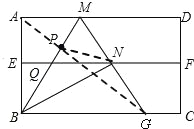
连接PN,PA,PG,
∵AB=![]() ,∠ABM=30°,
,∠ABM=30°,
∴BM=2,
∴BG=BM=2,
∴由折叠的性质知,点N与点A关于直线BM对称,
∴PN=PA,
∴PN+PG的最小值为AG,
∵AG=![]() ,
,
∴PN+PG的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
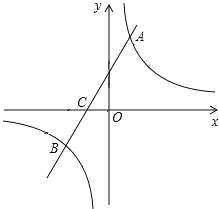
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在BC上,且CE=![]() BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=
BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=![]() S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
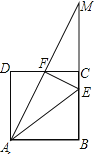
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com