
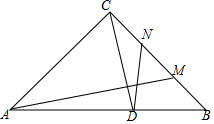
 已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN
已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN分析 (1)作BG⊥BC,交CD的延长线于G,AM交CD于O.首先证明△ACM≌△CBG,推出CM=BG,∠AMC=∠G,再证明△DBN≌△DBG,推出∠G=∠BND,推出∠AMC=∠DNB;
(2)(1)中结论仍然成立.证明方法类似(1).
解答 (1)证明:作BG⊥BC,交CD的延长线于G,AM交CD于O.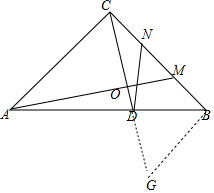
∵AM⊥CD,BG⊥BC,
∴∠AOC=∠CBG=∠ACM=90°,
∴∠ACO+∠CAO=90°,∠ACO+∠BCG=90°,
∴∠CAM=∠BCG,
∵AC=BC,
∴△ACM≌△CBG,
∴CM=BG,∠AMC=∠G,
∵CN=BM,
∴CM=BN=BG,
∵BD=BD,∠DBN=∠DBG=45°,
∴△DBN≌△DBG,
∴∠G=∠BND,
∴∠AMC=∠DNB;
(2)解:(1)中的结论成立.
理由:作BG⊥BC,交CD的延长线于G,AM交CD的延长线于O.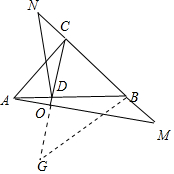
∵AM⊥CD,BG⊥BC,
∴∠AOC=∠CBG=∠ACM=90°,
∴∠ACO+∠CAO=90°,∠ACO+∠BCG=90°,
∴∠CAM=∠BCG,
∵AC=BC,
∴△ACM≌△CBG,
∴CM=BG,∠M=∠G,
∵CN=BM,
∴CM=BN=BG,
∵BD=BD,∠DBN=∠DBG=45°,
∴△DBN≌△DBG,
∴∠G=∠N,
∴∠M=∠N;
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 3a2-2a2=1 | B. | $\frac{1}{2}$a•2a2=a2 | C. | a6÷a2=a3 | D. | (-a2b)3÷(a3b)2=-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$且x≠0 | C. | x≥$\frac{1}{2}$ | D. | x>$\frac{1}{2}$且x≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
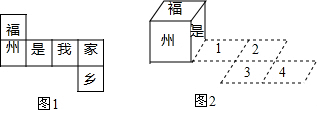
| A. | 家 | B. | 乡 | C. | 是 | D. | 福 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com