
分析 确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
解答 解:分式$\frac{b}{5{a}^{2}}$和$\frac{c}{2{a}^{3}}$的分母分别是5a2、2a3,故最简公分母是10a3;
故答案为:10a3.
点评 本题考查了最简公分母的定义及求法.通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.一般方法:①如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数,相同字母的最高次幂,所有不同字母都写在积里.②如果各分母都是多项式,就可以将各个分母因式分解,取各分母数字系数的最小公倍数,凡出现的字母(或含字母的整式)为底数的幂的因式都要取最高次幂.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
 如图,直线AB、CD、EF相交于点O.
如图,直线AB、CD、EF相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
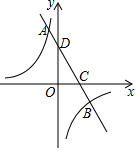 已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.
已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
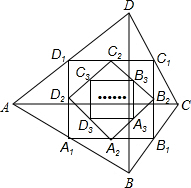 如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再各取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,以此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为21-n.
如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再各取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,以此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为21-n.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com