
如图,已知△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.连接BD交AE于M,连接CE交AB于N,BD与CE交点为F,连接AF.
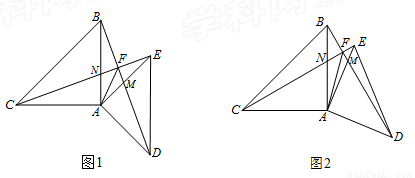
(1)如图1,求证:BD⊥CE;
(2)如图1,求证:FA是∠CFD的平分线;
(3)如图2,当AC=2,∠BCE=15°时,求CF的长.
(1)证明见试题解析;(2)证明见试题解析;(3)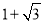 .
.
【解析】
试题分析:(1)证明△CAE≌△BAD即可;
(2)作AG⊥CE于G,AK⊥BD于K,由△CAE ≌△BAD,可以得到∠BFN=∠NAC=90°,即可得到BD⊥CE;
(3)先求出∠ACN =30°,再由含30°角的直角三角形的性质可以求出CF的长.
试题解析:(1)如图1

∵ ∠BAC =∠DAE=90°,∠BAE=∠BAE,∴ ∠CAE=∠BAD,在△CAE和△BAD中,
 ∴ △CAE≌△BAD.∴ ∠ACF=∠ABD,∵ ∠ANC=∠BNF,∴ ∠BFN=∠NAC=90°,∴ BD⊥CE;
∴ △CAE≌△BAD.∴ ∠ACF=∠ABD,∵ ∠ANC=∠BNF,∴ ∠BFN=∠NAC=90°,∴ BD⊥CE;
(2)如图1,

作AG⊥CE于G,AK⊥BD于K,由(1)知 △CAE ≌△BAD,∴ CE = BD,S△CAE =S△BAD .∴ AG = AK,∴ 点A在∠CFD的平分线上.即 FA是∠CFD的平分线;
(3)如图2

∵ ∠BAC = 90°,AB =AC,∴ ∠ACB=∠ABC =45°,∵ ∠BCE=15°,∴∠ACN =∠ACB-∠BCE= 30°=∠FBN,在Rt△ACN中,∵ ∠NAC = 90°,AC=2,∠ACN = 30°,∴AN= ,CN=
,CN= .∵ AB=AC=2,∴ BN=
.∵ AB=AC=2,∴ BN= .在Rt△ACN中,∵ ∠BFN = 90°,∠FBN = 30°,∴ NF=
.在Rt△ACN中,∵ ∠BFN = 90°,∠FBN = 30°,∴ NF=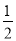 BN=
BN=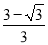 ,∴ CF=CN+NF=
,∴ CF=CN+NF=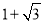 .
.
考点:1.全等三角形的判定与性质;2.含30度角的直角三角形.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
为了提高学生书写汉字的能力,某市举办了“汉字听写大赛”.为了决定谁将获得仅有的一张观赛券,小王和小李设计了如下的一个规则:不透明的甲袋中有编号分别为1,2,3的乒乓球三个,不透明的乙袋中有编号分别为4,5的乒乓球两个,五个球除了编号不同外,其他均相同.小王和小李分别从甲、乙两个袋子中随机地各摸出一个球,若所摸出的两个球上的数字之和为奇数,则小王去;若两个球上的数字之和为偶数,则小李去.试用列表法或画树状图的方法分析这个规则对双方是否公平?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:选择题
在△ABC中,锐角A、B满足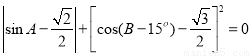 ,则△ABC是( )
,则△ABC是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.无法确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:填空题
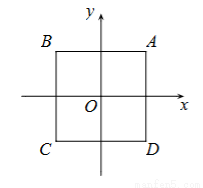
如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.写出一个函数 ,使它的图象与正方形ABCD有公共点,这个函数的表达式为 .
,使它的图象与正方形ABCD有公共点,这个函数的表达式为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,A,B,C是⊙O上的三个点,若∠C=35°,则∠AOB的度数为( )

A.35° B.55° C.65° D.70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知抛物线 .
.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若此抛物线与直线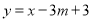 的一个交点在y轴上,求m的值.
的一个交点在y轴上,求m的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,已知点A(3,0),B(0,4),记Rt△OAB为三角形①,按图中所示的方法旋转三角形,依次得到三角形②,③,④,……,则三角形⑤的直角顶点的坐标为 ;三角形⑩的直角顶点的坐标为 ;第2015个三角形的直角顶点的坐标为 .
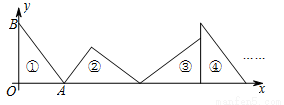 ?
?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省内江市八年级上学期期末考试数学试卷(解析版) 题型:选择题
下列运算正确的是( ).
A .(a²b)³=a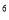 b³ B.a³·a²=a
b³ B.a³·a²=a C.a
C.a ÷a²=a D.a+a=a²
÷a²=a D.a+a=a²
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com