
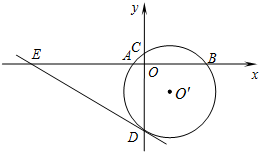
 如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.
如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.分析 (1)过点O′作O′F⊥DC,O′G⊥AB,根据点O′的坐标可知OF=OG,从而可知AB=CD;
(2)由垂径定理和勾股定理求得AG、BG、AF、DF的长度,然后由点O′的坐标可求得A、B、C、D四点的坐标;
(3)过点O′作O′F⊥CD,垂足为F,连接O′D.然后证明△O′FD∽△DOE,从而可求得点E的坐标,最后利用待定系数法求得DE的解析式即可.
解答 解:(1)如图1所示,过点O′作O′F⊥DC,O′G⊥AB
∵O′F⊥DC,O′G⊥AB,且点O′的坐标为(1,-1),
∴O′G=O′F=1.
∴AB=DC.
(2)如图2所示,过点O′作O′F⊥DC,O′G⊥AB,连接O′B,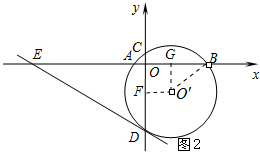
∵O′G⊥AB,
∴AG=BG.
在Rt△O′BG中,GB=$\sqrt{O′{B}^{2}-O′{G}^{2}}$=$\sqrt{(\sqrt{5})^{2}-{1}^{1}}$=2.
同理:FA=DF=2.
∴点A的坐标为(-1,0),点B的坐标为(3,0),点C的坐标为(1,0),点D的坐标为(-3,0).
(3)过点O′作O′F⊥CD,垂足为F,连接O′D.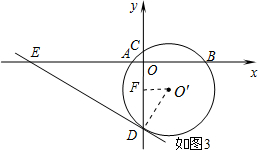
∵ED是圆O′的切线,
∴O′D⊥DE.
∴∠O′DF+∠ODE=90°.
∵∠DEO+∠EDO=90°,
∴∠CED=∠FDO′.
又∵∠EOD=∠O′FD=90°,
∴△O′FD∽△DOE.
∴$\frac{OD}{OE}=\frac{O′F}{FD}$,即$\frac{3}{OE}=\frac{1}{2}$.
解得:OE=6.
∴点E的坐标为(-6,0).
设DE的解析式为y=kx+b.
将x=-6,y=0;x=0,y=-3代入得解析式得;$\left\{\begin{array}{l}{-6k+b=0}\\{b=-3}\end{array}\right.$,
解得:k=$-\frac{1}{2}$,b=-3.
∴直线DE的解析式为y=$-\frac{1}{2}x-3$.
点评 本题主要考查的是圆的综合应用、相似三角形的性质和判定、勾股定理、待定系数法求一次函数的解析式,掌握有关圆的问题中常见辅助线的做法是解题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
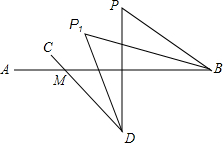 如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )| A. | 是一个定值 | B. | 有两个不同的值 | ||
| C. | 有三个不同的值 | D. | 有三个以上不同的值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com