
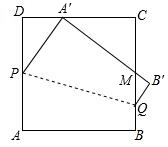
 如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点A′,使DA′=5,折痕为PQ,
如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点A′,使DA′=5,折痕为PQ,分析 (1)设PA=PA′=x,在Rt△DPA′中,由PD2+A′D2=PA′2,可得52+(12-x)2=x2,推出x=$\frac{169}{24}$,在Rt△ADA′中,AA′=$\sqrt{{5}^{2}+1{2}^{2}}$=13,推出AE=EA′=$\frac{13}{2}$,PE=$\sqrt{P{A}^{2}-A{E}^{2}}$=$\frac{65}{24}$,根据tan∠APE=$\frac{AE}{PE}$=$\frac{AG}{AP}$,可得$\frac{\frac{13}{2}}{\frac{65}{24}}$=$\frac{AG}{\frac{169}{24}}$,推出AG=$\frac{169}{10}$,由此即可解决问题.
(2)由△DA′P∽△CMA′,推出$\frac{PD}{CA′}$=$\frac{DA′}{CM}$,可得$\frac{\frac{119}{24}}{7}$=$\frac{5}{CM′}$,推出CM=$\frac{120}{17}$,由此即可解决问题.
解答 解:(1)设PA=PA′=x,在Rt△DPA′中,∵PD2+A′D2=PA′2,
∴52+(12-x)2=x2,
∴x=$\frac{169}{24}$,
在Rt△ADA′中,AA′=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴AE=EA′=$\frac{13}{2}$,PE=$\sqrt{P{A}^{2}-A{E}^{2}}$=$\frac{65}{24}$,
∴tan∠APE=$\frac{AE}{PE}$=$\frac{AG}{AP}$,
∴$\frac{\frac{13}{2}}{\frac{65}{24}}$=$\frac{AG}{\frac{169}{24}}$,
∴AG=$\frac{169}{10}$,
∴BG=AG-AB=$\frac{49}{10}$.
(2)∵∠DA′P+∠CA′M=90°,∠CA′M+∠CMA′=90°,
∴∠DA′P=∠A′MC,∵∠D=∠C=90°,
∴△DA′P∽△CMA′,
∴$\frac{PD}{CA′}$=$\frac{DA′}{CM}$,
∴$\frac{\frac{119}{24}}{7}$=$\frac{5}{CM′}$,
∴CM=$\frac{120}{17}$,
∴S△A′CM=$\frac{1}{2}$•CA′•CM=$\frac{1}{2}$×7×$\frac{120}{17}$=$\frac{420}{17}$.
点评 本题考查翻折变换、正方形的性质、相似三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,点E在AC的延长线上,已知AB∥CD,对于给出的四个结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠A=∠DCE;(4)∠D+∠ABD=180°,正确的有3个.
如图,点E在AC的延长线上,已知AB∥CD,对于给出的四个结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠A=∠DCE;(4)∠D+∠ABD=180°,正确的有3个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
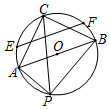 如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是4$\sqrt{3}$.
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
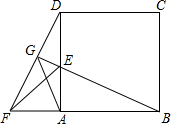 如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=3,EG=1,则线段AG的长为2$\sqrt{2}$.
如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=3,EG=1,则线段AG的长为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
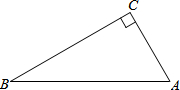 如图,在△ABC中,∠C=90°,∠A>∠B,请你用直尺和圆规作边AB的垂直平分线,交AB于点D,交BC于点E(要求:保留作图痕迹,不写作法)
如图,在△ABC中,∠C=90°,∠A>∠B,请你用直尺和圆规作边AB的垂直平分线,交AB于点D,交BC于点E(要求:保留作图痕迹,不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com