

���� ��1����ASA֤����BEF�ա�EMH�����ɵó�BE=ME��
��2������DE�����DE=ME���ɵ��������ε����ʵó�DH=MH=$\frac{1}{2}$DM=$\frac{3}{2}$��֤����AFH�ǵ���ֱ�������Σ��ɹ��ɶ������ɵó��𰸣�
��3��������������ɵ���ֱ�������ε����ʡ����ɶ�����ȫ�������ε����ʼ��ɵó��𰸣�
��� ��1��֤�������ı���ABCD�������Σ�
���BAD=��ADC=��BCD=��ABC=90�㣬��ACD=��BAC=45�㣬AD��BC��
��FH��AD��
���BFE=��BAD=90�㣬��EHM=��ADC=90�㣬
���CEH�ǵ���ֱ�������Σ��ı���BCHF�Ǿ��Σ�
��EH=CH��CH=BF��
��EH=BF��
��NE��EB��
���ɽǵĻ����ϵ�ã���EBF=��MEH��
�ڡ�BEF�͡�EMH�У�$\left\{\begin{array}{l}{��BFE=��EHM=90��}&{\;}\\{BF=EH}&{\;}\\{��EBF=��MEH}&{\;}\end{array}\right.$��
���BEF�ա�EMH��ASA����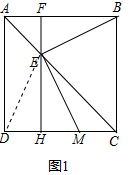
��BE=ME��
��2���⣺����DE����ͼ1��ʾ��
�ɣ�1���ã�BE=ME���ı���ADHF�Ǿ��Σ�
���AFH=90�㣬AF=DH��
�������εĶԳ��Եã�DE=BE��
��DE=ME��
��EH��DM��
��DH=MH=$\frac{1}{2}$DM=$\frac{3}{2}$��
��AF=$\frac{3}{2}$��
�ߡ�BAC=45�㣬��AFH=90�㣬
���AFH�ǵ���ֱ�������Σ�
��AE=$\sqrt{2}$AF=$\frac{3\sqrt{2}}{2}$��
��3���⣺��G������Ϊ��$\frac{13}{2}$��$\frac{1}{2}$����$\frac{7}{2}$��$\frac{5}{2}$�����������£�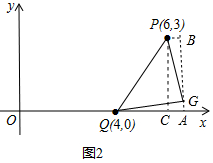
�ٵ���G�ڵ�P���Ҳ�ʱ��
��G��GA��x����A����P��PB��x�ᣬPB��GA��B����PC��x����C����ͼ2��ʾ��
��P��6��3����Q��4��0����
��OQ=4��OC=6��PC=3��
��CQ=6-4=2��
��PQ=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$��
�ߡ�PQGΪ����ֱ�������Σ���PGQ=90�㣬
��GQ=GP=$\frac{\sqrt{13}}{\sqrt{2}}$=$\frac{\sqrt{26}}{2}$��
�ɽǵĻ����ϵ�ã���AQG=��BGP��
�ڡ�AQG�͡�BGP�У�$\left\{\begin{array}{l}{��GAQ=��PBG=90��}&{\;}\\{��AQG=��BGP}&{\;}\\{GQ=PG}&{\;}\end{array}\right.$��
���AQG�ա�BGP��AAS����
��AG=BP��AQ=BG��
��AG=BP=x��AQ=BG=y����$\left\{\begin{array}{l}{x+y=3}\\{{x}^{2}+{y}^{2}=\frac{13}{2}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{5}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{1}{2}}\end{array}\right.$����ȥ����
��AG=$\frac{1}{2}$��AQ=$\frac{5}{2}$��
��OA=OQ+AQ=4+$\frac{5}{2}$=$\frac{13}{2}$��
��G��$\frac{13}{2}$��$\frac{1}{2}$����
�ڵ�G�ڵ�P�����ʱ��ͬ���ã�G��$\frac{7}{2}$��$\frac{5}{2}$����
������������G��������$\frac{13}{2}$��$\frac{1}{2}$����$\frac{7}{2}$��$\frac{5}{2}$����
���� �������ı����ۺ���Ŀ�������������ε����ʡ�ȫ�������ε��ж������ʡ����������ε����ʡ�����ֱ�������ε��ж������ʡ����ɶ������ⷽ�����֪ʶ�������ۺ���ǿ����һ���Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$cm | B�� | 2$\sqrt{2}$cm | C�� | $\sqrt{3}$cm | D�� | $\sqrt{6}$cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{20}$ | B�� | $\sqrt{12}$ | C�� | $\sqrt{42}$ | D�� | $\sqrt{32}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | -1 | C�� | -1��-3 | D�� | 1��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��x��3 | B�� | -1��x��3 | C�� | x��3 | D�� | x��-1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com