
| A.(1,2) | B.(-1,-2) | C.(2,-1) | D.(1,-2) |
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:不详 题型:解答题
 的图象。
的图象。
 的图象;
的图象;
|
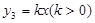 ,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .
,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题
 与挖掘时间
与挖掘时间 之间的关系如图所示,请根据图象所提供的信息解答下列问题:
之间的关系如图所示,请根据图象所提供的信息解答下列问题:
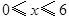 的时段内,
的时段内, 与
与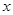 之间的函数关系式;
之间的函数关系式;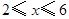 的时段内,
的时段内, 与
与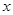 之间的函数关系式;
之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
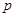 和
和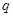 (
(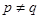 ),构成函数
),构成函数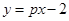 和
和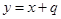 ,并使这两个函数图象的交点在直线
,并使这两个函数图象的交点在直线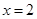 的右侧,则这样的有序数对(
的右侧,则这样的有序数对(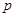 ,
,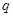 )共有( )
)共有( )| A.7对 | B.9对 | C.11对 | D.13对 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题
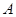 种布料
种布料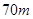 ,
,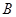 种布料
种布料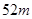 ,现计划用这两种布料生产
,现计划用这两种布料生产  、
、 两种型号的时装共
两种型号的时装共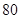 套。已知做一套
套。已知做一套 型号的时装需用
型号的时装需用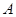 种布料
种布料 ,
,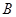 种布料
种布料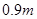 ,可获利润
,可获利润 元;做一套
元;做一套 型号的时装需用
型号的时装需用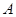 种布料
种布料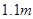 ,
,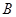 种布料
种布料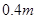 ,可获利润
,可获利润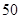 元。若设生产
元。若设生产 型号的时装套数为
型号的时装套数为 ,用这批布料生产这两种型号的时装所获得的总利润为
,用这批布料生产这两种型号的时装所获得的总利润为 元。
元。 (元)与
(元)与 (套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
(套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
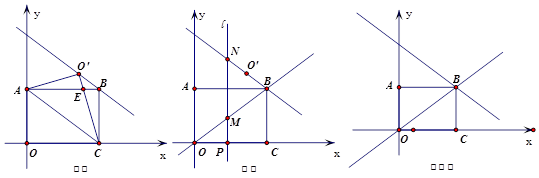
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com