Question

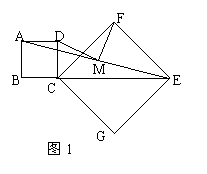
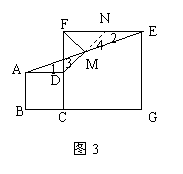
如图1，操作：把正方形CGEF的对角线

CE放在正方形ABCD的边BC的延长线上（CG＞BC），

取线段AE的中点M。

探究：线段MD、MF的关系，并加以证明。

说明：（1）如果你经历反复探索，没有找到解决问题

的方法，请你把探索过程中的某种思路写出来（要求

至少写3步）；（2）在你经历说明（1）的过程之后，

可以从下列①、②、③中选取一个补充或更换已知条件，

完成你的证明。

注意：选取①完成证明得10分；选取②完成证明得

7分；选取③完成证明得5分。

①     DM的延长线交CE于点N，且AD＝NE；

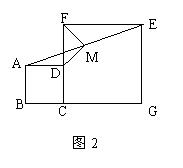
②     将正方形CGEF绕点C逆时针旋转45°（如图2），

其他条件不变；③在②的条件下且CF＝2AD。

Answer 1

关系是：MD=MF，MD⊥MF。

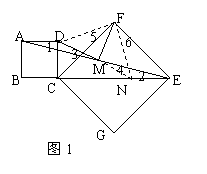
证法一：如图1，延长DM交CE于N，连结

       FD、FN。

       ∵正方形ABCD，∴AD∥BE，AD=DC

       ∴∠1＝∠2。

又∵AM=EM，∠3＝∠4，

∴△ADM≌△ENM

∴AD=EN，MD=MN。

∵AD=DC，∴DC=NE。

又∵正方形CGEF，

∴∠FCE=∠NEF=45°，FC=FE，∠CFE=90°。

又∵正方形ABCD，∴∠BCD＝90°。

∴∠DCF=∠NEF=45°，

∴△FDC≌△FNE。

∴FD=FN，∠5＝∠6

∵∠CFE＝90°，∴∠DFN＝90°。

又∵DM=MN，∴MD=MF，DM⊥MF。

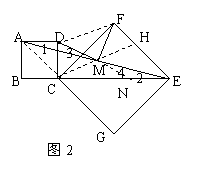
   证法二：如图2，连结AC、FD，延长DM交CE于N，连结

           CM并延长交FE于H。

           ∵正方形ABCD，∴AD∥BE。∴∠1＝∠2。

           ∵AM=EM，∠3＝∠4，

∴△ADM≌△ENM

∴MD=MN。

∵AC和CE分别是正方形ABCD和CGEF的对角线，

∴∠ACB=∠FEC=45°，∠FCN＝45°，

∴AC∥EF。同理可证△ACM≌△EHM。

∴CM=MH。

∵正方形ABCD和正方形CGEF，

∴∠DCN＝∠CFH=90°，

∴MC＝MD＝MN＝MF＝MH。

∴点D、C、N、F在以点M为圆心，MD为半径的圆上，

∠FDN=∠DFM。

∴∠FDN＝∠FCN＝45°，∴∠FDN＝∠DFM＝45°。

∴MD=MF，DM⊥MF。

   证法三：如图2，同证法二证出MC＝MD＝MN＝MF＝MH。

          ∴∠MCN=∠MNC，∠MCF=∠MFC。

          ∵∠DMC＝∠MCN＋∠MNC=2∠MCN，

∠FMH＝∠MCF＋∠MFC＝2∠MCF。

∴∠DMC+∠FMH=2∠MCN+∠MCF＝2（∠MCN+∠MCF）

＝2∠FCE=90°

∴∠DMF＝180°－90°＝90°，∴DM⊥FM。

思路一：

∵正方形ABCD、CGEF，∴AB=BC=CD=AD，

∠B=∠BCD=∠CDA=∠BAD＝90°

CF=EF=EG=CG，∠G=∠GEF=∠EFC=∠FCG=90°，

∠FCE=∠FEC=45°

∴∠DCF=∠FEC。

思路二：

延长DM交CE于N。

∵正方形ABCD、CGEF，∴AD∥CE，∴∠DAM=∠NEM。

又∵∠DMA＝∠NME，AM=EM，

∴△ADM≌△ENM。

思路三：

∵正方形CGEF，∴∠FCE=∠FEC＝45°。

又∵正方形ABCD，∴∠DCF=180°－∠DCB－∠FCE＝45°，

∠DCF＝∠FEC＝45°

选取条件①

证明：如图1，∵正方形ABCD∴AD∥BE，AD=DC，

     ∴∠1＝∠2

     ∵AD=NE，∠3=∠4，

     ∴△ADM≌△ENM。

     ∴MD=MN。

   又∵AD=DC，∴DC=NE。

   又∵正方形CGEF，∴FC=FE，∠FCE=∠FEN＝45°。

     ∴∠FCD=∠FEN=45°。

     ∴△FDC≌△FNE。

     ∴FD=FN，∠5＝∠6，∴∠DFN=∠CFE＝90°。

      ∴MD=MF，MD⊥MF。

选取条件②

证明：如图3，延长DM交FE于N。

∵正方形ABCD、CGEF，

∴CF=EF，AD=DC，∠CFE=90°，AD∥FE

∴∠1＝∠2

又∵MA＝ME，∠3＝∠4

∴△AMD≌△EMN

∴MD=MN，AD=EN。∵AD=DC，∴DC=NE。

又∵FC=FE，∴FD=FN。

又∵∠DFN=90°，∴FM⊥MD，MF=MD。

选取条件③

证明：如图3，延长DM交FE于N。

∵正方形ABCD、CGEF，

∴CF=EF，AD=DC，∠CFE=90°，AD∥FE

∴∠1＝∠2

又∵MA＝ME，∠3＝∠4

∴△AMD≌△EMN

∴AD=EN，MD=MN，∵CF=2AD，EF=2EN，

∴FD=FN。又∵∠DFN＝90°，∴FM⊥MD，MF=MD。