
阅读材料,数学家高斯在读书时曾经研究过这样一个问题: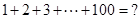
经过研究,这个问题的一般性结论是: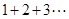
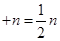
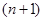 ,其中
,其中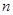 是正整数.
是正整数.
现在我们来研究一个类似的问题:
观察下面三个特殊的等式:
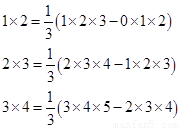
将这三个等式的两边分别相加,可以得: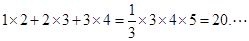
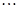
读完这段材料,请你思考后回答:
(1)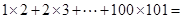 ___________________ ;
___________________ ;
(2)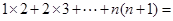 ______________________ ;
______________________ ;
(3)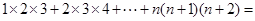 ___________ .
___________ .
科目:初中数学 来源: 题型:
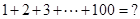
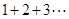
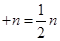
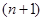 ,其中
,其中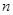 是正整数.
是正整数.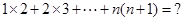
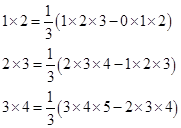
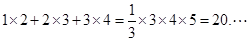
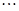
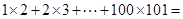 ___________________ ;
___________________ ; 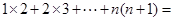 ______________________ ;
______________________ ; 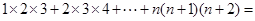 ___________ .
___________ . 查看答案和解析>>
科目:初中数学 来源:湖北省期中题 题型:解答题
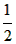 n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+n(n+1)=?
n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+n(n+1)=?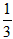 (1×2×3-0×1×2)
(1×2×3-0×1×2)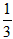 (2×3×4-1×2×3)
(2×3×4-1×2×3)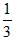 (3×4×5-2×3×4)
(3×4×5-2×3×4)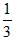 ×3×4×5=20;
×3×4×5=20;查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读材料,数学家高斯在上学时曾经研究过这样一个问题,1+2+3+…+10=?
经过研究,这个问题的一般性结论是1+2+3+…+n=![]() n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
观察下面三个特殊的等式:
1×2=![]() (1×2×3-0×1×2)
(1×2×3-0×1×2)
2×3=![]() (2×3×4-1×2×3)
(2×3×4-1×2×3)
3×4=![]() (3×4×5-2×3×4)
(3×4×5-2×3×4)
将这三个等式的俩边相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20.
×3×4×5=20.
读完这段材料,请你计算:
(1)1×2+2×3+…+100×101;(只需写出结果)(2分)
(2)1×2+2×3+…+ n(n+1);(写出计算过程) (5分)
(3)1×2×3+2×3×4+…+ n(n+1)(n+2).(只需写出结果)(3分)
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读材料,数学家高斯在上学时曾经研究过这样一个问题,1+2+3+…+10=?
经过研究,这个问题的一般性结论是1+2+3+…+n=![]() n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
观察下面三个特殊的等式:
1×2=![]() (1×2×3-0×1×2)
(1×2×3-0×1×2)
2×3=![]() (2×3×4-1×2×3)
(2×3×4-1×2×3)
3×4=![]() (3×4×5-2×3×4)
(3×4×5-2×3×4)
将这三个等式的俩边相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20.
×3×4×5=20.
读完这段材料,请你计算:
(1)1×2+2×3+…+100×101;(只需写出结果)(2分)
(2)1×2+2×3+…+ n(n+1);(写出计算过程) (5分)
(3)1×2×3+2×3×4+…+ n(n+1)(n+2).(只需写出结果)(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com