
【题目】如图,在□ABCD中,AB=2 BC=4,点E、F分别是BC、AD的中点.
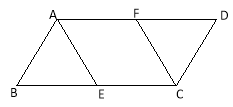
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
【答案】见试题解析
【解析】
试题分析:(1)根据平行四边形的性质得出AB=CD,∠B=∠D,AD=BC,又因为点E、F分别是BC、AD的中点,所以BE=DF,得出△ABE≌△CDF.(2)取BC的中点G,连接AG,根据菱形的性质得出AE=CE= BE=AB,
∴△ABE是等边三角形. 根据勾股定理求出CG的长,根据面积公式即可求出菱形的面积.
试题解析:(1)证明:在平行四边形ABCD中,点E、F分别是BC、AD的中点,
∴BE=DF, ![]() ,AB=CD,∴△ABE≌△CDF.
,AB=CD,∴△ABE≌△CDF.
(2)解:取BE的中点G,,连接AG.
当四边形AECF为菱形时,AE=CE= BE=AB,∴△ABE是等边三角形.
![]()
又∵EC=2, ∴菱形AECF的面积=EC×AG=2×![]() =2
=2![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
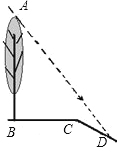
【题目】如图,坡面CD的坡比为![]() ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是![]() 米,则小树AB的高是 米.
米,则小树AB的高是 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )

A.不变 B.增大 C.减小 D.先变大再变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
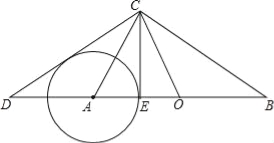
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题: 
为了丰富社会实践活动,引导学生科学探究,学校组织七年级同学走进中国科技馆,亲近科学,感受科技魅力.来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④号小球向下运动,运动速度均为3米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为2米/秒,当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚 ![]() 秒到达相应位置,问②号小球运动了多少米?
秒到达相应位置,问②号小球运动了多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com