
【题目】已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A,B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,那个说明理由.
【答案】
(1)
解:解方程x2﹣4x﹣12=0得x1=﹣2,x2=6,
即A(﹣2,0),B(6,0)
(2)
解:将A、B两点坐标代入二次函数y=ax2+bx+6,
得到 ![]() ,
,
解得  ,
,
即y=﹣ ![]() x2+2x+6,
x2+2x+6,
由于y=﹣ ![]() x2+2x+6=
x2+2x+6= ![]() (x﹣2)2+8,
(x﹣2)2+8,
即抛物线的对称轴为x=2,顶点坐标为(2,8)
(3)
解:如图,作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,
∵C(0,6),
∴C′(4,6),
设直线AC′解析式为y=kx+n,
则 ![]() ,
,
解得 ![]() ,
,
∴y=x+2,
当x=2时,y=4,
即P(2,4).

【解析】(1)解一元二次方程x2﹣4x﹣12=0,求出点A和点B的横坐标,进而得到答案;(2)将A、B两点坐标代入二次函数y=ax2+bx+6,得到a和b的二元一次方程组,求出a和b的值即可,进而求出顶点坐标;(3)作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,求出C′坐标,求出直线AC′解析式,进而求出点P的坐标.
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本,需要知道一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车为1440辆;当每辆次小车的停车费超过5元时,每增加1元,到此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费一每天的固定支出)
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.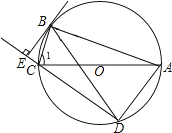
(1)求证:∠1=∠BAD;
(2)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.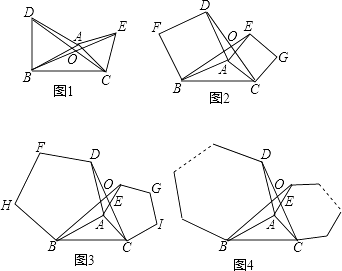
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如图(1),在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求S正方形MNPQ . 问题探究:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图(2)).
(1)若将上述四个等腰三角形拼成一个新的正方形(无缝隙,不重叠),则新正方形的边长为;这个新正方形与原正方形ABCD的面积有何关系;(填“>”,“=”“或<”);通过上述的分析,可以发现S正方形MNPQ与S△FSB之间的关系是:
(2)问题解决:求S正方形MNPQ .
(3)拓展应用:如图(3),在等边△ABC各边上分别截取AD=BE=CF=1,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△PQR,求S△PQR . (请仿照上述探究的方法,在图3的基础上,先画出图形,再解决问题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( ![]() )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( ![]() )海里.
)海里.
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(参考数据: ![]() =1.41,
=1.41, ![]() =1.73,
=1.73, ![]() =2.45)
=2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com