
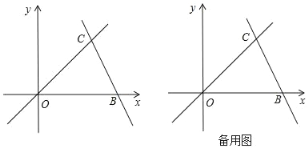
����Ŀ����ͼ��ֱ��OC��BC�ĺ�����ϵʽ�ֱ�Ϊy��x��y����2x+b���ҽ���C�ĺ�����Ϊ2������P��x��0�����߶�OB���ƶ���0��x��3����
��1�����C�������b��
��2������A��0��1������xΪ��ֵʱ��AP+CP��ֵ��С��
��3������P��ֱ��EF��x�ᣬ�ֱ�ֱ��OC��BC�ڵ�E��F��
����EF��3�����P�����꣮
�����OBC��λ��ֱ��EF��ಿ�ֵ����Ϊs����д��s��x֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
���𰸡���1��b��6����2����![]() ��0������3����P��1��0������s��
��0������3����P��1��0������s��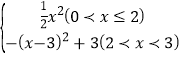 ��
��
��������
��1������C�ĺ��������ֱ��y=x�У������C���꣬��������C�������ֱ��BC����ʽ�У��������b��
��2�������öԳ���ȷ������C'�����꣬����AC'�ó���P��λ�ã����ô���ϵ�������ֱ��AC'�Ľ���ʽ���ɵó����ۣ�
��3���������ֱ��BC����ʽ�������ó���E��F�����꣬�����ó�EF�������EF=3����������⼴�ɵó����ۣ�
�ڷ�������������������ε������ʽ������IJ�ɵó����ۣ�
��1���ߵ�C��ֱ��OC��y��x�ϣ��ҵ�C�ĺ�����Ϊ2
���C��2��2����
�ߵ�C��ֱ��BC��y����2x+b�ϣ�
����2��2+b��2��
��b��6��
��2����ͼ1������C����x��ĶԳƵ�C��������AC'��x���ڵ�P����ʱAP+CP��AP+PC'��AC'��С��
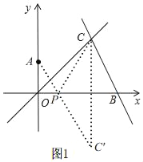
��C��2��2������C'��2����2����
�ߵ�A��0��1����
��ֱ��AC'�Ľ���ʽΪy����![]() x+1��
x+1��
��y��0��
��0����![]() x+1��
x+1��
��x��![]() ��
��
���P��������![]() ��0����
��0����
��3�����ɣ�1��֪��b��6��
��ֱ��BC�Ľ���ʽΪy����2x+6��
��EF��x����P��
��F��x����2x+6����
�ߵ�E��ֱ��OC�ϣ�
��E��x��x����
��EF��|��2x+6��x|��|3x��6|��
��EF��3��
��|3x��6|��3��
��x��3���ᣩ��x��1��
��P��1��0����
�ڵ�0��x��2ʱ����ͼ2��
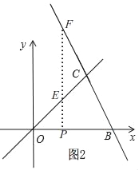
��E��x��x����
��OP��x��PE��x��
��s��S��OPE��![]() OP��PE��
OP��PE��![]() x2��
x2��
��2��x��3ʱ����ͼ3��
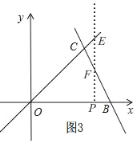
�ɣ�2��֪��ֱ��BC�Ľ���ʽΪy����2x+6��
��B��3��0����
��P��x��0����
��F��x����2x+6����
��BP��3��x��PF����2x+6��
��s��S��OBC��S��BPF��![]() ��3��2��
��3��2��![]() ��3��x������2x+6��������x��3��2+3��
��3��x������2x+6��������x��3��2+3��
����s��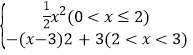 .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨ������ɲ�����ֻ��еľ��������㳵����ʻ���ٶȣ����õľ��鹫ʽ��u=16![]() ������u��ʾ���٣���λ��km/h����d��ʾɲ�����루��λ��m����f��ʾĦ��ϵ������һ�ν�ͨ�¹��У����d=20m��f=1.44����������ͨ�¹ʵ�·������Ϊ80km/h�����������Ƿ�Υ�泬����ʻ��˵�����ɣ����ο����ݣ�
������u��ʾ���٣���λ��km/h����d��ʾɲ�����루��λ��m����f��ʾĦ��ϵ������һ�ν�ͨ�¹��У����d=20m��f=1.44����������ͨ�¹ʵ�·������Ϊ80km/h�����������Ƿ�Υ�泬����ʻ��˵�����ɣ����ο����ݣ�![]() ��1.4��
��1.4��![]() ��2.2��
��2.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ӧ���⣺
��ij��������Ϊ17.6m2���������ǡ����110����ͬ�������ε�ש�̳ɣ�ÿ���ש�ı߳��Ƕ��٣�
����֪��һ��������ˮ����ⳤ��60cm���ڶ���������ˮ�������ȵ�һ��ˮ��������3������81000 cm3����ڶ���ˮ����Ҫ��Ƥ����ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����EΪ����ABCD��BC�ߵ��е㣬����F�ڶԽ���AC���˶�������BF��EF����AF=x����BEF���ܳ�Ϊy����ô�ܱ�ʾy��x�ĺ�����ϵ�Ĵ���ͼ���ǣ� ��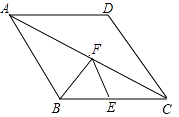
A.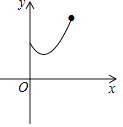
B.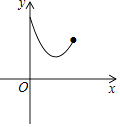
C.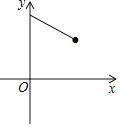
D.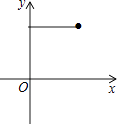
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������9�֣�
����Ҫ����������⣮
��1������Ҫ����������⣮
������x2��2x��1��0�Ľ�Ϊ________________________��
������x2��3x��2��0�Ľ�Ϊ________________________��
������x2��4x��3��0�Ľ�Ϊ________________________��
���� ����
��2���������Ϸ�����������������������룺
������x2��9x��8��0�Ľ�Ϊ________________________��
������x�ķ���________________________�Ľ�Ϊx1��1��x2��n��
��3�������䷽���ⷽ��x2��9x��8��0������֤������۵���ȷ�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ǰ�һ����Բ�������ߵ�һ����Χ�ɵķ��ͼ�γ�Ϊ����Բ������֪��A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬�����ߵĽ���ʽΪy=(x-1)2-4��ABΪ��Բ��ֱ�������������Բ����y��صõ���CD�ij� �� 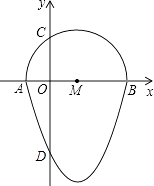
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�ĶԽ���BD��һ��M�ֱ���ƽ���ı������ߵ�ƽ����EF��GH����ôͼ�е�AEMG�����S1��HCFM�����S2�Ĵ�С��ϵ��( )
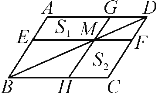
A. S1��S2 B. S1��S2 C. S1��S2 D. 2S1��S2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() �ڵ�
�ڵ�![]() ����
����![]() ������
������![]() ��һ�㣬����
��һ�㣬����![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ���ҽ�ֱ��
���ҽ�ֱ��![]() �ڵ�
�ڵ�![]() ��
��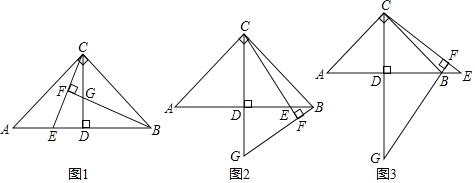
��1����ͼ1������![]() ���߶�
���߶�![]() ��ʱ����֤��
��ʱ����֤��![]() ��
��
��2����ͼ2������![]() ���߶�
���߶�![]() ��ʱ�������������䣬�����
��ʱ�������������䣬�����![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
��3����ͼ3������![]() ���߶�
���߶�![]() ���ӳ�����ʱ�������������䣬��ֱ��д��
���ӳ�����ʱ�������������䣬��ֱ��д��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD����CAE��AB��AD��AC��AE����E��F��C��D��ͬһֱ���ϣ�
��1����֤����ABC�ա�ADE��
��2������B��30�㣬��BAC��100�㣬��F��CE���е㣬����AF�����FAE�Ķ�����
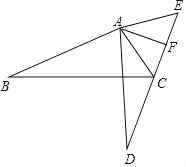
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com