
分析 (1)a-$\frac{1}{a}$=±$\sqrt{(a-\frac{1}{a})^{2}}$,根据完全平方公式得出a-$\frac{1}{a}$=±$\sqrt{(a+\frac{1}{a})^{2}-4a•\frac{1}{a}}$,代入求出即可;
(2)求出$\sqrt{a}$<$\frac{1}{\sqrt{a}}$,根据完全平方公式和已知得出($\sqrt{a}$)2-2•$\sqrt{a}$•$\frac{1}{\sqrt{a}}$+($\frac{1}{\sqrt{a}}$)2=3-2•$\sqrt{a}$•$\frac{1}{\sqrt{a}}$,求出即可.
解答 解:(1)∵a+$\frac{1}{a}$=3,
∴a-$\frac{1}{a}$
=±$\sqrt{(a-\frac{1}{a})^{2}}$
=±$\sqrt{(a+\frac{1}{a})^{2}-4a•\frac{1}{a}}$
=±$\sqrt{{3}^{2}-4}$
=$±\sqrt{5}$,
故答案为:±$\sqrt{5}$;
(2)∵0<a<1,
∴$\sqrt{a}$<$\frac{1}{\sqrt{a}}$,
∵a+$\frac{1}{a}$=3,
∴($\sqrt{a}$)2-2•$\sqrt{a}$•$\frac{1}{\sqrt{a}}$+($\frac{1}{\sqrt{a}}$)2=3-2•$\sqrt{a}$•$\frac{1}{\sqrt{a}}$,
∴($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2=1,
∴$\sqrt{a}$-$\frac{1}{\sqrt{a}}$=-1,
故答案为:-1.
点评 本题考查了完全平方公式的应用,能灵活运用公式进行变形是解此题的关键,注意:完全平方公式有:①a2-2ab+b2=(a-b)2,②a2-2ab+b2=(a-b)2.


科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中复习数学检测试卷(一)(解析版) 题型:单选题
把多项式x2+ax+b分解因式,得(x+1)(x-3)则a,b的值分别是( )
A. a=2,b=3 B. a=-2,b=-3 C. a=-2,b=3 D. a=2,b=-3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
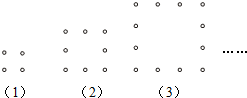
| 图形编号 | 1 | 2 | 3 | 4 | 5 | … |
| 棋子个数 | 4 | 8 | 12 | 16 | 20 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
把多项式x2+ax+b分解因式,得(x+1)(x-3)则a,b的值分别是( )
A. a=2,b=3 B. a=-2,b=-3 C. a=-2,b=3 D. a=2,b=-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com