
| |||||||||||
(1) |
联立 |
(2) |
解:在x轴上存在满足条件的点P,其坐标为P1(-2 当OA=OP时,因为OA= 当AO=AP时,过A作AQ⊥x轴于Q(如图),所以PQ=OQ=2,所以P点坐标为(4,0) 当PA=PO时,P在AO的垂直平分线上,所以P点的坐标为(5,0).
解题指导:A点是抛物线y=x2与直线y=2x的交点,所以联立这两个函数的关系式,组成方程组来求;要使△AOP为等腰三角形,这里OA是已知边,因此,要对OA进行分类讨论(OA为底或OA为腰). |


科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:013
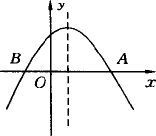
如图所示,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,且![]() ,则m等于
,则m等于
A.![]()
B.0
C.![]() 或0
或0
D.1
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:013
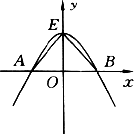
如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A,B,E,且△ABE是等腰直角三角形,AE=BE,则下列式子不能总成立的是
A.b=0
B.S△ABE=c2
C.ac=-1
D.a+c=0
查看答案和解析>>
科目:初中数学 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:013
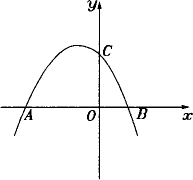
如图所示,抛物线y=ax2+bx+c与x轴相交于点A,B,与y轴相交于点C,如果OB=OC=![]() OA,那么b的值为
OA,那么b的值为
A.-2
B.-1
C.-![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源:2009年辽宁省本溪市中考数学试题及答案 题型:022
如图所示,抛物线y=ax2+bx+c(a≠0)与x轴的两个交点分别为A(-1,0)和B(2,0),当y<0时,x的取值范围是________.
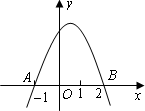
查看答案和解析>>
科目:初中数学 来源:山东省菏泽市2010年初中学业水平考试数学试题 题型:059
如图所示,抛物线y=ax2+bx+c经过原点O,与x轴交于另一点N,直线y=kx+4与两坐标轴分别交于A、D两点,与抛物线交于B(1,m)、C(2,2)两点.

(1)求直线与抛物线的解析式.
(2)若抛物线在x轴上方的部分有一动点P(x,y),设∠PON=α,求当△PON的面积最大时tanα的值.
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△POA的面积等于△PON面积的![]() ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com