
【题目】如图所示,抛物线![]() 交
交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于点C,直线
轴于点C,直线![]() 经过点A、C.
经过点A、C.
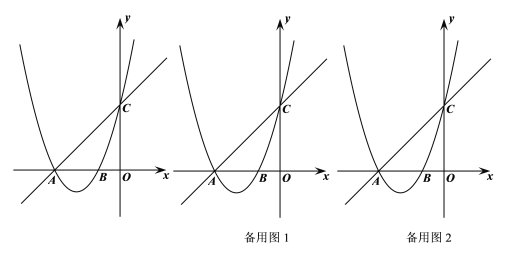
(1)求抛物线的解析式;
(2)点P为直线AC上一点,在平面内是否存在点Q,使得以A、B、P、Q为顶点的四边形为正方形?若存在,求出点Q的坐标,若不存在,请说明理由;
(3)在![]() 轴上存在点M,且
轴上存在点M,且![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
【答案】(1)![]() ;(2)存在,点Q的坐标为
;(2)存在,点Q的坐标为![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)分别求得函数![]() 与两坐标轴的交点,确定A,C两点的坐标,然后利用待定系数法求二次函数解析式;
与两坐标轴的交点,确定A,C两点的坐标,然后利用待定系数法求二次函数解析式;
(2)先求得抛物线与x轴交点,确定AB的长,然后分四边形ABPQ,四边形APBQ为正方形两种情况,结合正方形的性质求得Q点坐标;
(3)分点M在点A的右侧和点M在点A的左侧,根据题意及等腰三角形的性质求得∠MCO=30°或60°,从而利用三角函数求解.
解:(1)对于![]()
令![]() ,则
,则![]() ,解之得:
,解之得:![]()
令![]() ,则
,则![]()
∴![]()
把![]() 分别代入
分别代入![]() 得
得![]()
解之得![]()
∴抛物线的解析式为![]()
(2)存在,理由如下
令![]() ,解之得:
,解之得:![]()
∴![]()
∴![]()
分为两种情况:
①当四边形ABPQ为正方形时,如图1所示
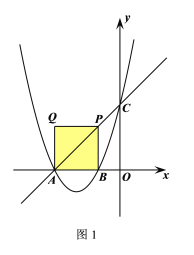
对于![]() ,当
,当![]() 时,
时,![]()
∴点P在直线![]() 上
上
∵![]() 轴
轴
∴![]()
②当四边形APBQ为正方形时,如图2所示

连结PQ,则![]()
∴![]()
∴![]()
对于![]() ,当
,当![]() 时,
时,![]()
∴点P在直线![]() 上
上
易知点P、Q关于![]() 轴对称
轴对称
∴![]()
综上所述,点Q的坐标为![]() 或
或![]()
(3)![]() 或
或![]()
①当点M在点A的右侧时,如图3所示
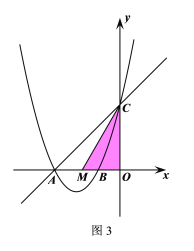
∵![]()
∴![]()
∴△AOC为等腰直角三角形
∴![]()
∴![]()
∴![]()
在Rt△COM中
∵![]()
∴![]()
∴![]()
②当点M在点A的左侧时,如图4所示

![]()
在Rt△COM中
∵![]()
∴![]()
∴![]()
综上所述,点M的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a≠0)的图象如图所示,
(a≠0)的图象如图所示,
有下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魔术师说将你想到的数进行以下四步操作,我就可以猜到你心里想的数.
第一步:心中想一个数,求其平方;
第二步:想比这个数小2的数,求其平方;
第三步:求其平方的差值;
第四步:平方的差值除以4再加1.
将结果告诉我,我就能猜中你心里想的数.
(1)若你想的数是5,求出你告诉魔术师的结果是多少.
(2)聪明的同学们,你觉得魔术师的步骤一定能猜中你心中的数吗?请用代数式计算证明你的结论.
解答:魔术师 猜中你心中的数(填“能”或“否”);
证明:设心中想的数为![]() (
(![]() 为任意实数)
为任意实数)
查看答案和解析>>
科目:初中数学 来源: 题型:
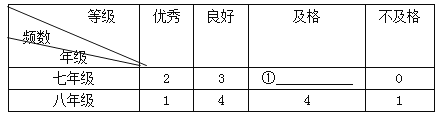
【题目】《中学生体质健康标准》规定的等级标准为:90分及以上为优秀,80~89分为良好,60~79分为及格,59分及以下为不及格.某校为了解七、八年级学生的体质健康情况,现从两年级中各随机抽取10名同学进行体质健康检测,并对成绩进行分析.成绩如下:
七年级 | 80 | 74 | 83 | 63 | 90 | 91 | 74 | 61 | 82 | 62 |
八年级 | 74 | 61 | 83 | 91 | 60 | 85 | 46 | 84 | 74 | 82 |
(1)根据上述数据,补充完成下列表格中序号.
整理数据:
分析数据:
年级 | 平均数 | 众数 | 中位数 |
七年级 | ②_________ | 74 | 77 |
八年级 | 74 | 74 | ③____________ |
(2)该校目前七年级有300人,八年级有200人,试估计两个年级体质健康等级达到优秀的学生共有多少人?
(3)结合上述数据信息,你认为哪个年级学生的体质健康情况更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC内接于⊙O,且AB为⊙O的直径,作![]() 的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.
的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.

(1)求证:△ABD为等腰直角三角形;
(2)填空:
①若![]() ,则AE的长度为_______;
,则AE的长度为_______;
②在①的条件下,延长AC、DB交于点P,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x=![]() 与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<
与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<![]() 时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是
时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是

A. ②③④ B. ①②③ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
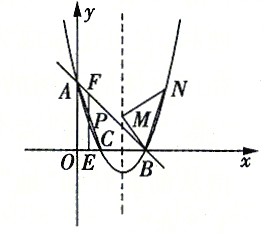
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业承接了27000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com