
| A. | $\left\{\begin{array}{l}a=2\\ b=3.\end{array}\right.$ | B. | $\left\{\begin{array}{l}a=-2\\ b=3.\end{array}\right.$ | C. | $\left\{\begin{array}{l}a=2\\ b=-3.\end{array}\right.$ | D. | $\left\{\begin{array}{l}a=-2\\ b=-3.\end{array}\right.$ |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 重庆实验外国语学校坐落在美丽的“华岩寺”旁边,它被誉为“巴山灵境”.我校实践活动小组准备利用测角器和所学的三角函数知识去测“华岩寺”大佛的高度.他们在A处测得佛顶P的仰角为45°,继而他们沿坡度为i=3:4的斜坡AB前行25米到达大佛广场边缘的B处,BQ∥AC,PQ⊥BQ,在B点测得佛顶P的仰角为63°,则大佛的高度PQ为( )米.
重庆实验外国语学校坐落在美丽的“华岩寺”旁边,它被誉为“巴山灵境”.我校实践活动小组准备利用测角器和所学的三角函数知识去测“华岩寺”大佛的高度.他们在A处测得佛顶P的仰角为45°,继而他们沿坡度为i=3:4的斜坡AB前行25米到达大佛广场边缘的B处,BQ∥AC,PQ⊥BQ,在B点测得佛顶P的仰角为63°,则大佛的高度PQ为( )米.| A. | 15 | B. | 20 | C. | 25 | D. | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
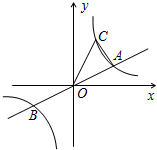 如图,已知直线y=ax与双曲线$y=\frac{k}{x}(k>0)$交于A、B两点,点B的坐标为B(-2,-1),C为双曲线$y=\frac{k}{x}(k>0)$上一点,且在第一象限内.
如图,已知直线y=ax与双曲线$y=\frac{k}{x}(k>0)$交于A、B两点,点B的坐标为B(-2,-1),C为双曲线$y=\frac{k}{x}(k>0)$上一点,且在第一象限内.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=3$\sqrt{2}$,BC=9,则DF等于( )
如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=3$\sqrt{2}$,BC=9,则DF等于( )| A. | $\frac{9}{4}$ | B. | $\frac{7}{2}$ | C. | 4 | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系内,已知点A的位置;点B与点(-3,-1)关于原点O对称;将点A向下平移5个单位到达点C.
如图,在平面直角坐标系内,已知点A的位置;点B与点(-3,-1)关于原点O对称;将点A向下平移5个单位到达点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com