
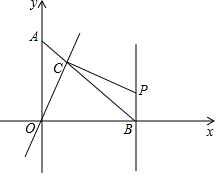
 如图,点A(0,a ),点B( b,0 )且满足a2+2b2-2ab-2b+1=0.经过原点O的直线l交线段AB于点C,过C作OC⊥CP,与直线BP相交于点P,BP⊥OB.现将直线l绕O点旋转,使交点C从A向B运动,但P点必须在第一象限内,分析此图后,对下列问题作出探究:
如图,点A(0,a ),点B( b,0 )且满足a2+2b2-2ab-2b+1=0.经过原点O的直线l交线段AB于点C,过C作OC⊥CP,与直线BP相交于点P,BP⊥OB.现将直线l绕O点旋转,使交点C从A向B运动,但P点必须在第一象限内,分析此图后,对下列问题作出探究:分析 (1)根据a2+2b2-2ab-2b+1=0,运用非负数的性质,即可得出a=b=1,进而得到点A、B的坐标;
(2)先过点C作x轴的平行线,分别交OA、BP于点T、H.根据△CHB为等腰直角三角形,以及四边形OBHT为矩形,得到OT=CH,进而根据AAS,判定△OTC≌△CHP,从而得出OC=CP;
(3)先根据四边形CDBH是矩形,得到CD=BH,再根据△BCD是等腰直角三角形,得出CD=BD,然后根据四边形CDOT是矩形,△OTC≌△CHP,即可得到OD=HP,最后得出OB+PB=OD+DB+BP=HP+BP+DB=BH+BD=2CD;
(4)根据P点必须在第一象限内,可得只有当∠BCP=∠CBP=45°时,△BCP为等腰直角三角形,据此得到点C与点A重合,此时BP=CP=1,故当△PBC为等腰三角形时,c=1.
解答 解:(1)∵a2+2b2-2ab-2b+1=0,
∴(a-b)2+(b-1)2=0,
∴a=b=1,
∴A(0,1 ),B( 1,0 );
(2)OC=CP.
证明:如图,过点C作x轴的平行线,分别交OA、BP于点T、H.
∵PC⊥OC,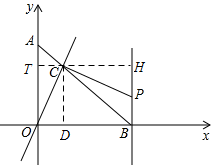
∴∠OCP=90°,
∵OA=OB=1,
∴∠OBA=45°,
∵TH∥OB,
∴∠BCH=45°,
又∵∠CHB=90°,
∴△CHB为等腰直角三角形,
∴CH=BH,
∵∠AOB=∠OBH=∠BHT=90°,
∴四边形OBHT为矩形,
∴OT=BH,
∴OT=CH,
∵∠TCO+∠PCH=90°,∠CPH+∠PCH=90°,
∴∠TCO=∠CPH,
∵HB⊥x轴,TH∥OB,
∴∠CTO=∠PHC=90°,
在△OTC和△CHP中,
$\left\{\begin{array}{l}{∠TCO=∠CPH}\\{∠CTO=∠PHC}\\{OT=CH}\end{array}\right.$,
∴△OTC≌△CHP(AAS),
∴OC=CP;
(3)2CD=OB+PB,理由:
过C作CD⊥OB于点D,则∠CDB=∠DBH=∠BHC=90°,
∴四边形CDBH是矩形,
∴CD=BH,
又∵∠ABO=45°,
∴△BCD是等腰直角三角形,
∴CD=BD,
∵∠CDO=∠TOD=∠OTC=90°,
∴四边形CDOT是矩形,
∴OD=TC,
由(2)可得,△OTC≌△CHP,
∴TC=HP,
∴OD=HP,
∴OB+PB=OD+DB+BP=HP+BP+DB=BH+BD=2CD;
(4)当点C与点A重合时,CP⊥AO,
此时,∠PCB=45°,BP=CP=1,即P(1,1);
当点C为AB 中点时,点P与点B重合,
此时,CP与CB重合,即P(1,0),
∵P点必须在第一象限内,
∴0°<∠BCP≤45°,
∵∠CBH=45°,
∴只有当∠BCP=∠CBP=45°时,△BCP为等腰直角三角形,
∴当△PBC为等腰三角形时,c=1.
故答案为:1.
点评 本题属于三角形综合题,主要考查了等腰直角三角形的性质,非负数的性质,全等三角形的判定与性质,矩形的判定与性质以及等腰三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形以及等腰直角三角形,根据全等三角形的对应边相等以及矩形的对边相等进行推导.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1440毫升 | B. | 1.4×103毫升 | C. | 0.14×104毫升 | D. | 14×102毫升 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 变为原来的5倍 | B. | 变为原来的10倍 | C. | 变为原来的$\frac{1}{5}$ | D. | 不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com