
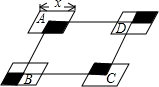
 如图,平行四边形ABCD的边长AD为8,面积为32,四个全等的小平行四边形对称中心分别在平行四边形ABCD的顶点上,它们的各边与平行四边形ABCD的各边分别平行,且与平行四边形ABCD相似.若平行四边形的一边长为x,且0<x≤8,阴影部分的面积和为y,则y与x之间的函数关系的大致图象是( )
如图,平行四边形ABCD的边长AD为8,面积为32,四个全等的小平行四边形对称中心分别在平行四边形ABCD的顶点上,它们的各边与平行四边形ABCD的各边分别平行,且与平行四边形ABCD相似.若平行四边形的一边长为x,且0<x≤8,阴影部分的面积和为y,则y与x之间的函数关系的大致图象是( )| A. | 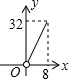 | B. | 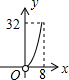 | C. | 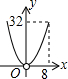 | D. | 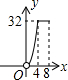 |
分析 根据平行四边形的中心对称性可知四块阴影部分的面正好等于一个小平行四边形的面积,再根据相似多边形面积的比等于相似比的平方列式求出y与x之间的函数关系式,然后根据二次函数图象解答.
解答 解:∵四个全等的小平行四边形对称中心分别在?ABCD的顶点上,
∴阴影部分的面积等于一个小平行四边形的面积,
∵小平行四边形与?ABCD相似,
∴$\frac{y}{32}$=($\frac{x}{8}$)2,
整理得y=$\frac{1}{2}$x2,
又0<x≤8,
只有B选项图象符合y与x之间的函数关系的大致图象.
故选:B.
点评 本题考查了动点问题的函数图象,根据平行四边形的对称性与相似多边形的面积的比等于相似比的平方求出y与x的函数关系是解题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
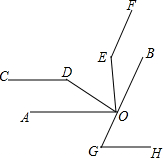 已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.
已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
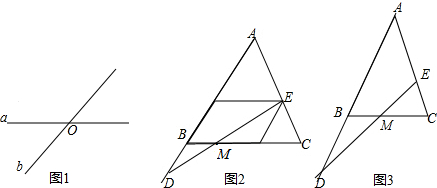
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com