
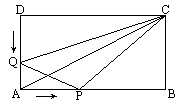
如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向B以2cm/s速度移动;点Q沿DA边从点D开始向A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:(1)当t为何值时,△QAP为等腰直角三角形?(2)求四边形QAPC的面积,并提出一个与计算结果有关的结论;(3)当t为何值时,以Q、A、P为顶点的三角形与△ABC相似?
|
解答:(1)对于任何时刻t,AP=2t,DQ=t,QA=6-t,当AQ=AP时,△QAP为等腰直角三角形,即6-t=2t,解得t=2,所以,当t=2s时,△QAP为等腰直角三角形. (2)在△QAC中,QA=6-t,QA边上的高DC=12,所以S△QAC= 由计算结果发现: 在P、Q两点移动过程中,四边形QAPC的面积始终保持不变.(也可提出:P、Q两点到对角线AC的距离之和保持不变). (3)根据题意,可分为两种情况研究. ①当 ②当 分析:(1)已知∠PAQ= |
|
注意:相似三角形作为数学的一个重大分支,是中考的必考内容,题型包括选择、填空、解答,涉及的内容广而全,而以相似三角形为背景的综合题更是常见的热点题型. |


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
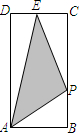 如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )
如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )A、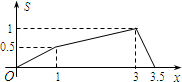 | B、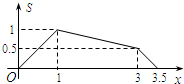 | C、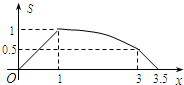 | D、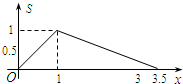 |
查看答案和解析>>
科目:初中数学 来源: 题型:
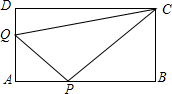 P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.
P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
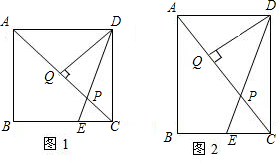 B=nBC
B=nBC| CP |
| PQ |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
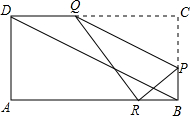
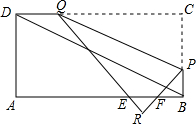
 如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.
如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com