
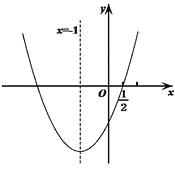
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列5个结论:①
,下列5个结论:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正确的结论为________________.(注:只填写正确结论的序号)
,其中正确的结论为________________.(注:只填写正确结论的序号)
【答案】②④.
【解析】
根据抛物线开口方向得到a>0,根据抛物线对称轴为直线x=-![]() =-1得到b=2a,则b>0,根据抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;由x=
=-1得到b=2a,则b>0,根据抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;由x=![]() ,y=0,得到
,y=0,得到![]() a+
a+![]() b+c=0,即a+2b+4c=0;由a=
b+c=0,即a+2b+4c=0;由a=![]() b,a+b+c>0,得到
b,a+b+c>0,得到![]() b+2b+c>0,即3b+2c>0;由x=-1时,函数最大小,则a-b+c<m2a-mb+c(m≠1),即a-b≤m(am-b).
b+2b+c>0,即3b+2c>0;由x=-1时,函数最大小,则a-b+c<m2a-mb+c(m≠1),即a-b≤m(am-b).
解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴为直线x=-![]() =-1,
=-1,
∴b=2a,则2a-b=0,所以③错误;
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵x=![]() 时,y=0,
时,y=0,
∴![]() a+
a+![]() b+c=0,即a+2b+4c=0,所以②正确;
b+c=0,即a+2b+4c=0,所以②正确;
∵a=![]() b,a+b+c>0,
b,a+b+c>0,
∴![]() b+2b+c>0,即3b+2c>0,所以④正确;
b+2b+c>0,即3b+2c>0,所以④正确;
∵x=-1时,函数最大小,
∴a-b+c<m2a-mb+c(m≠1),
∴a-b≤m(am-b),所以⑤错误.
故答案为②④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师对大学说:“你任意想一个非零实数,然后按下列步骤操作,我会直接说出你运算的最后结果”
操作步骤如下:
第一步:计算这个数与1的和的平方,减去这个数与1的差的平方
第二步:把第一步得到的数乘以25
第三步:把第二步得到的数除以你想的这个数
(1)若小明同学心里想的是数9,请帮他计算出最后结果:
![]() .
.
(2)老师说:“同学们,无论你们心里想的是什么非零实数,按照以上步骤进行操作,得到的最后结果都相等”,小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 为二次函数
为二次函数![]() 的图象的顶点.
的图象的顶点.
(1)过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,求线段
,求线段![]() 的最小值;
的最小值;
(2)设正比例函数![]() 与上述二次函数的图象相交于点
与上述二次函数的图象相交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是李老师在黑板上演示的尺规作图及其步骤,
已知钝角![]() ,尺规作图及步骤如下:
,尺规作图及步骤如下:
步骤一:以点![]() 为圆心,
为圆心,![]() 为半径画弧;
为半径画弧;
步骤二:以点![]() 为圆心,
为圆心,![]() 为半径画弧,两弧交于点
为半径画弧,两弧交于点![]() ;
;
步骤三:连接![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.

下面是四位同学对其做出的判断:
小明说:![]() ;
;
小华说:![]() ;
;
小强说:![]() ;
;
小方说:![]() .
.
则下列说法正确的是( )
A.只有小明说得对B.小华和小强说的都对
C.小强和小方说的都不对D.小明和小方说的都对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点(可与
上一点(可与![]() ,
,![]() 重合),以点
重合),以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() (其中
(其中![]() ).
).
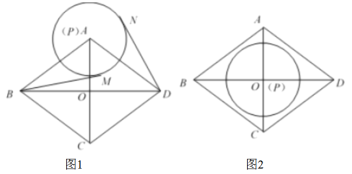
(1)如图1,当点![]() 与
与![]() 重合,且
重合,且![]() 时,过点
时,过点![]() ,
,![]() 分别作
分别作![]() 的切线,切点分别为
的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 与点
与点![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 内部时(不含边界),求
内部时(不含边界),求![]() 的取值范围;
的取值范围;
(3)当点![]() 为
为![]() 或
或![]() 的内心时,直接写出
的内心时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b交x轴于点A(1,0) ,与双曲线![]() 交于点
交于点![]()
(1)求直线AB的解析式为____ ____________;
(2)若 x 轴上存在动点 M(m,0),过点 M 且与 x 轴垂直的直线与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC >BD时,写出m的取值范围_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
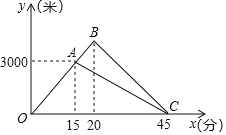
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com