【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．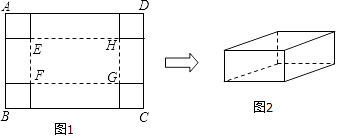
（1）当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；
（2）当EH：EF=7：2，且侧面积与底面积之比为9：7时，求x的值．
【答案】
（1）解：∵矩形纸板ABCD的一边长为90cm，
∴矩形纸板的另一边长为3600÷90=40（cm），
则S侧=2[x（90﹣2x）+x（40﹣2x）]=﹣8x2+260x，
=﹣8（x﹣ 
）2+ 
．
∵﹣8＜0，
∴当x= 时，S侧最大=
（2）解：设EF=2m，则EH=7m，
则侧面积为2（7mx+2mx）=18mx，底面积为7m2m=14m2，
由题意，得18mx：14m2=9：7，
∴m=x．
则AD=7x+2x=9x，AB=2x+2x=4x
由4x9x=3600，且x＞0，
∴x=10
【解析】（1）最值问题可运用函数思想解决，设出自变量x,函数为纸盒的侧面积y,构建二次函数，配成顶点式，求出最大值；（2）用x的代数式表示出侧面积与底面积，根据9：7，再根据总面积为3600，建立方程，求出x.
科目：初中数学 来源： 题型：
【题目】小红同学在做作业时，遇到这样一道几何题：
已知：AB∥CD∥EF，∠A＝110°，∠ACE＝100°，过点E作EH⊥EF,垂足为E，交CD于H点．
（1）依据题意，补全图形；
（2）求∠CEH的度数．
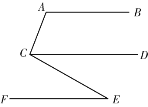
小明想了许久对于求∠CEH的度数没有思路，就去请教好朋友小丽，小丽给了他如图2所示的提示：
请问小丽的提示中理由①是 ；
提示中②是： 度；
提示中③是： 度；
提示中④是： ，理由⑤是 ．
提示中⑥是 度；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】操作探究：
（1）实践：如图1， 
中，
为
边上的中线，
的面积记为
，
的面积记为
．则
．
（2）探究：在图2中，
、
分别为四边形
的边、的中点，四边形的面积记为
，阴影部分面积记为
，则和之间满足的关系式为______：
（3）解决问题：
在图3中，、
、、
分别为任意四边形的边、
、、
的中点，并且图中阴影部分的面积为
平方厘米，求图中四个小三角形的面积和，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】乘法公式的探究与应用：
（1）如图甲，边长为a的大正方形中有一个边长为b的小正方形，请你写出阴影部分的面积是
（2）小颗将阴影部分接下来，重新拼成一个长方形，如图乙，则长方形的长是 ，宽是 ，面积是 （写成多项式乘法的形式）．
（3）比较甲乙两图阴影部分的面积，可以得到恒等式
（4）运用你所得到的公式计算：10.3×9.7．
（5）若49x2﹣y2＝25，7x﹣y＝5，则7x+y的值为
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了绿化环境，某中学八年级（3班）同学都积极参加了植树活动，下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图：
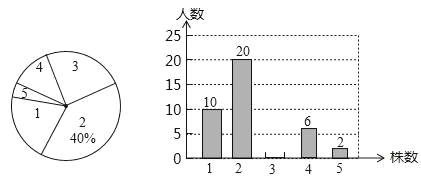
请根据以上统计图中的信息解答下列问题．
（1）植树3株的人数为 ；
（2）扇形统计图中植树为1株的扇形圆心角的度数为 ；
（3）该班同学植树株数的中位数是
（4）小明以下方法计算出该班同学平均植树的株数是：（1+2+3+4+5）÷5＝3（株），根据你所学的统计知识
判断小明的计算是否正确，若不正确，请写出正确的算式，并计算出结果
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如下命题中：（1）过一点有且只有一条直线与已知直线垂直；（2）垂线段最短；（3）过一点有且只有一条直线与这条直线平行；（4）内错角相等；（5）平行于同一直线的两直线平行；（6）有两个角互余的三角形是直角三角形是真命题的有（ ）
A.
个B.
个C.
个D.
个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
，点
为平面内一点.
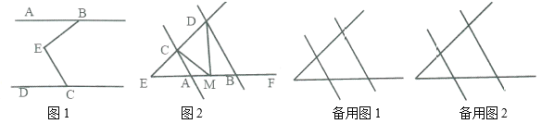
（1）如图1，
和
互余，小明说过作
，很容易说明
。请帮小明写出具体过程；
（2）如图2，，当点在线段
上移动时（点与
，
两点不重合），指出
与，的数量关系？请说明理由；
（3）在（2）的条件下，若点在，两点外侧运动（点与
，，三点不重合）请直接写出与，的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
