
【题目】如图,△ABC中,D是BC的中点,过点D的直线GF交AC于F,交AC的平行线BG于G点,DE⊥GF,交AB于点E,连接EG,EF.

(1)说明:BG=CF;
(2)BE,CF与EF这三条线段能否组成一个三角形?
【答案】见解析
【解析】
(1)由BG∥AC得出∠DBG=∠DCF,从而利用ASA得出△BGD与△CFD全等,进一步证得结论
(2)根据△BGD与△CFD全等得出GD=FD,BG=CF,再又因为DE⊥GF,从而得出EG=EF,从而进一步得出结论
(1)∵BG∥AC
∴∠DBG=∠DCF
又∵D为BC中点
∴BD=CD
又∵∠BDG=∠CDF
∴△BGD![]() △CFD(ASA)
△CFD(ASA)
∴BG=CF
(2)能
证明如下:
∵△BGD![]() △CFD
△CFD
∴BG=CF,GD=DF
又∵DE⊥GF
∴GE=EF
∵BE,BG,GE组成了△BGE
∴BE,BG,GE三边满足三角形三边的关系
同理,与BG,GE相等的两边CF,EF与BE三条线段亦满足三角形三边关系
∴BE,CF,EF这三条线段可以组成三角形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
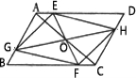
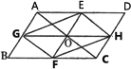
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,![]() ,
,![]() ,点
,点![]() 为
为![]() 反向延长线上一点(图中所有角均指小于
反向延长线上一点(图中所有角均指小于![]() 的角).下列结论:①
的角).下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正.确.结论的个数有( ).
.其中正.确.结论的个数有( ).
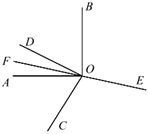
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
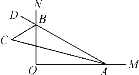
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家自2016年1月1日起实行全面放开二胎政策,某计生组织为了解该市家庭对待这项政策的态度,准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取1 000户家庭调查;
B.从一个城镇的不同住宅楼中随机选取1 000户家庭调查;
C.从该市公安局户籍管理处随机抽取1 000户城乡家庭调查.
(1)在上述调查方式中,你认为比较合理的一个是【1】.(填“A”、“B”或“C”)
(2)将一种比较合理的调查方式调查得到的结果分为四类:(A)已有两个孩子;
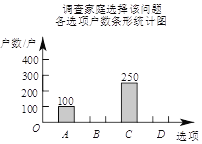
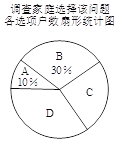
(B)决定生二胎;(C)考虑之中;(D)决定不生二胎.将调查结果绘制成如下两幅不完整的统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
①补全条形统计图.
②估计该市100万户家庭中决定不生二胎的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
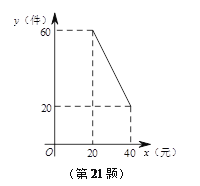
【题目】某超市以20元/件的价格购进一批商品,根据前期销售情况,每天销售量y(件)与该商品的销售价x(元)之间的函数图象如图所示.
(1)求y与x之间的函数关系式.
(2)如果将该商品的销售价定为30元/件,不考虑其它因素,求该超市每天销售这种商品所能获得的利润.
(3)直接写出能使该超市获得最大利润的商品销售价
查看答案和解析>>
科目:初中数学 来源: 题型:
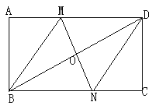
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D.E分别在边AB,AC上,DE∥BC,按下列要求画图并填空
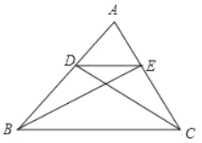
(1)过点E画直线BC的垂线交直线BC于点F;
(2)点D到直线______的距离等于线段EF的长度
(3)联结BE.CD,EBC的面积______DBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形 ABCD,其中,NH=NG 1cm ,设 BF acm .
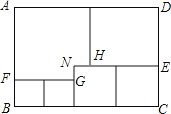
(1)用含 a 的代数式分别表示 CE,DE;
(2)求长方形 ABCD 的周长.(用含 a 的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com