
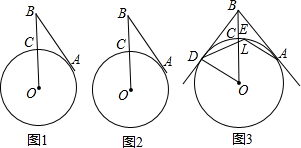
分析 (1)根据直角三角形30度角性质,可知BO=2OA,由此即可证明.
(2)如图2中,连接OA,设BC=2a,OC=3a,利用勾股定理求出AB,根据tan∠OBA=$\frac{OB}{AB}$,即可解决问题.
(3)首先证明DL=AM,求出DO、OB、DM,再根据△DOB∽△AMD,$\frac{AM}{DO}$=$\frac{DM}{OB}$即可解决问题.
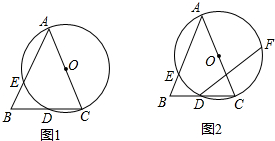
解答 解:(1)如图1中,连接AC、OA.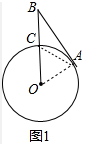
∵AB是⊙O切线,
∴OA⊥AB,
∴∠OAB=90°,
∵∠B=30°,
∴OB=2AO,
∵OB=OC+BC,
∴BC=CO.
(2)如图2中,连接OA,设BC=2a,OC=3a,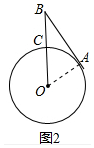
∵AB是⊙O切线,
∴OA⊥AB,
∴∠OAB=90°,
在Rt△AOB中,∵∠OAB=90°,BO=5a,OA=3a,
∴AB=$\sqrt{O{B}^{2}-A{O}^{2}}$=$\sqrt{(5a)^{2}-(3a)^{2}}$=4a,
∴tan∠ABO=$\frac{OA}{BA}$=$\frac{3a}{4a}$=$\frac{3}{4}$.
(3)如图3中,连接AD、延长DO交⊙O于M,连接AM.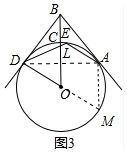
∵AL∥DM,
∴∠DAL=∠ADM,
∴$\widehat{DL}$=$\widehat{AM}$,
∴DL=AM,
∵BD、BA是⊙O切线,
∴∠OBD=∠OBA,BD=AB=8,∠ODB=90°,
∵tan∠OBD=tan∠OBA=$\frac{3}{4}$,
∴DO=6,BO=$\sqrt{B{D}^{2}+D{O}^{2}}$=10,
∵DM是直径,
∴∠DAM=∠ODB=90°,
∵OB⊥AD,MA⊥AD,
∴OB∥AM,
∴∠BOD=∠M,
∴△DOB∽△AMD,
∴$\frac{AM}{DO}$=$\frac{DM}{OB}$
∴$\frac{AM}{6}$=$\frac{12}{10}$,
∴AM=$\frac{36}{5}$,
∴DL=AM=$\frac{36}{5}$.
点评 本题考查圆的综合题、直角三角形30度角性质、锐角三角函数的定义、相似三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com