
 OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
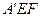 ,求△
,求△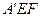 与五边形OEFBC重叠部分的面积.
与五边形OEFBC重叠部分的面积.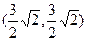
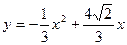
 或1或
或1或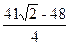
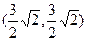 . (2分)
. (2分)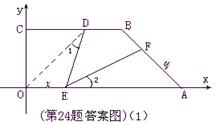
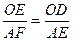 ,即:
,即: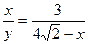
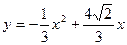 (6分)
(6分)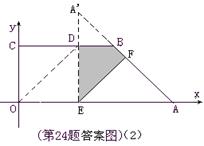
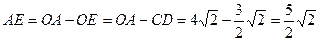
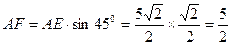
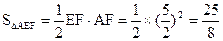
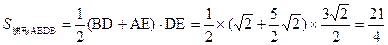
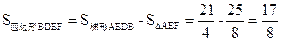 (也可用
(也可用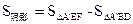 ) (8分)
) (8分)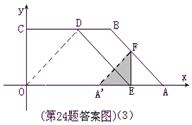

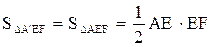
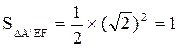 (10分)
(10分)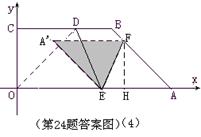
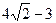
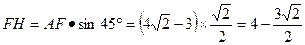
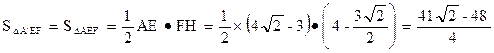
 或1或
或1或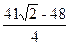 (12分)
(12分)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形
年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形 (如图
(如图 所示),
所示), ,
, 为水面,点
为水面,点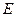 在
在 上,测得背水坡
上,测得背水坡 的长为
的长为 米,倾角
米,倾角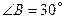 ,迎水坡
,迎水坡 上线段
上线段 的长为
的长为 米,
米, .
.
 米,参考数据
米,参考数据 );
); 天?(精确到
天?(精确到 米)
米)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
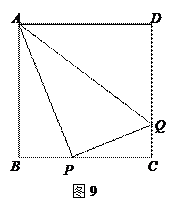
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com