
分析 (1)首先化简二次根式进而合并同类二次根式求出即可;
(2)直接利用二次根式乘除运算法则化简求出即可.
解答 解:(1)2$\sqrt{27}$-$\sqrt{48}$+$\sqrt{\frac{1}{3}}$
=2×3$\sqrt{3}$-4$\sqrt{3}$+$\frac{\sqrt{3}}{3}$
=$\frac{7\sqrt{3}}{3}$;
(2)$\sqrt{2\frac{1}{3}}$×$\sqrt{\frac{3}{5}}$$÷\sqrt{1\frac{2}{5}}$
=$\sqrt{\frac{7}{3}×\frac{3}{5}×\frac{5}{7}}$
=1.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
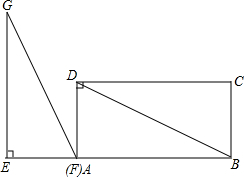 如图,在矩形ABCD中,DB=6,AD=3,在Rt△EFG中,∠GEF=90°,EF=3,GF=6,△EFG(点F和点A重合)的边EF和矩形的边AB在同一直线上.现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,解答下列问题:
如图,在矩形ABCD中,DB=6,AD=3,在Rt△EFG中,∠GEF=90°,EF=3,GF=6,△EFG(点F和点A重合)的边EF和矩形的边AB在同一直线上.现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 清晨,小强沿着一个如图所示的六边形广场周围的小路,按顺时针方向跑步
清晨,小强沿着一个如图所示的六边形广场周围的小路,按顺时针方向跑步查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com