
【题目】如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:![]() ,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() 取1.73.
取1.73.
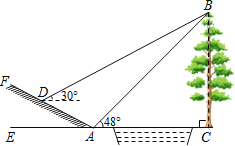
【答案】树高BC约12.5米.
【解析】
首先过点D作DM⊥BC于点M,DN⊥AC于点N,由FA的坡比i=1:![]()
,DA=6,可求得AN与DN的长,然后设大树的高度为x,又由在斜坡上A处测得大树顶端B的仰角是48°,可得AC=![]() ,又由在△BDM中
,又由在△BDM中![]() ,,可得x﹣3=(3
,,可得x﹣3=(3![]() +
+![]() )
)![]() ,继而求得答案.
,继而求得答案.
过点D作DM⊥BC于点M,DN⊥AC于点N,
则四边形DMCN是矩形,
∵DA=6,斜坡FA的坡比i=1:![]() ,
,
∴DN=![]() AD=3,AN=ADcos30°=6×
AD=3,AN=ADcos30°=6×![]() =3
=3![]() ,
,
设大树的高度为x,
∵在斜坡上A处测得大树顶端B的仰角是48°,
∴tan48°=![]() ≈1.11,
≈1.11,
∴AC=![]() ,
,
∴DM=CN=AN+AC=3![]() +
+![]() ,
,
∵在△BDM中,![]() ,
,
BM=![]() DM,
DM,
∴x﹣3=(3![]() +
+![]() )
)![]() ,
,
解得:x≈12.5.
答:树高BC约12.5米.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车从甲地驶向乙地,慢车从乙地驶向甲地,两车同时出发并且在同一条公路上匀速行驶,途中快车休息1.5小时,慢车没有休息.设慢车行驶的时间为x小时,快车行驶的路程为![]() 千米,慢车行驶的路程为
千米,慢车行驶的路程为![]() 千米.如图中折线OAEC表示
千米.如图中折线OAEC表示![]() 与x之间的函数关系,线段OD表示
与x之间的函数关系,线段OD表示![]() 与x之间的函数关系.
与x之间的函数关系.
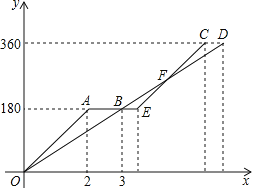
请解答下列问题:
(1)求快车和慢车的速度;
(2)求图中线段EC所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)线段OD与线段EC相交于点F,直接写出点F的坐标,并解释点F的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
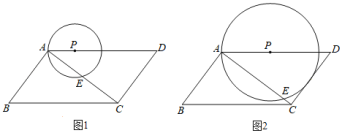
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)线段AC的长度是 .
(2)如图2,当⊙P与边CD相切于点F时,求AP的长;
(3)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程对承接了60万平方米的绿化工程,由于情况有变,……,设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳绳是大家喜闻乐见的一项体育运动,集体跳绳时,需要两人同频甩动绳子,当绳子甩到最高处时,其形状可近似看作抛物线.如图是小明和小亮甩绳子到最高处时的示意图,两人拿绳子的手之间的距离为![]() ,离地面的高度为
,离地面的高度为![]() ,以小明的手所在位置为原点,建立平面直角坐标系.
,以小明的手所在位置为原点,建立平面直角坐标系.
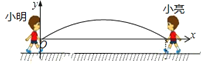
(1)当身高为![]() 的小红站在绳子的正下方,且距小明拿绳子手的右侧
的小红站在绳子的正下方,且距小明拿绳子手的右侧![]() 处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
(2)若身高为![]() 的小丽也站在绳子的正下方.
的小丽也站在绳子的正下方.
①当小丽在距小亮拿绳子手的左侧![]() 处时,绳子能碰到小丽的头吗?请说明理由;
处时,绳子能碰到小丽的头吗?请说明理由;
③设小丽与小亮拿绳子手之间的水平距离为![]() ,为保证绳子不碰到小丽的头顶,求
,为保证绳子不碰到小丽的头顶,求![]() 的取值范围.(参考数据:
的取值范围.(参考数据:![]() 取3.16)
取3.16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ;⑥
;⑥![]() . 其中正确的个数是( )
. 其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发以lcm/s的速度沿折线AC﹣CB运动,过点P作PQ⊥AB于点Q,当点P不与点A、B重合时,以线段PQ为边向右作正方形PQRS,设正方形PQRS与△ABC的重叠部分面积为S,点P的运动时间为t(s).
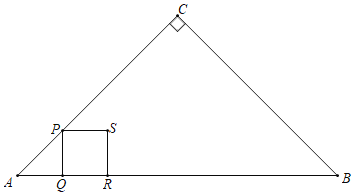
(1)用含t的代数式表示CP的长度;
(2)当点S落在BC边上时,求t的值;
(3)当正方形PQRS与△ABC的重叠部分不是五边形时,求S与t之间的函数关系式;
(4)连结CS,当直线CS分△ABC两部分的面积比为1:2时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com